题目内容
【题目】已知函数f（x）=
（a∈R）是奇函数．
（1）求实数a的值；
（2）判断并证明f（x）在R上的单调性．
【答案】（1）
；（2）证明见解析．
【解析】
（1）根据题意，由奇函数的定义可得f（﹣x）＝﹣f（x），即
，变形分析可得答案；
（2）根据题意，由（1）的结论可得函数f（x）的解析式，设x1＜x2，由作差法分析可得结论．
（1）根据题意，函数f（x）
（a∈R）是奇函数，
则有f（﹣x）＝﹣f（x），
即，变形可得a＝1；
（2）由（1）的结论，f（x）
2x﹣2﹣x，则R上为增函数，
证明如下：设x1＜x2，
f（x1）﹣f（x2）＝（
）﹣（
）＝（
）（1
），
又由x1＜x2，则（）＜0，（1）＞0，
则f（x1）﹣f（x2）＜0，
则函数f（x）在R上为增函数．
课时掌控随堂练习系列答案
一课一练一本通系列答案
浙江之星学业水平测试系列答案
【题目】某同学用“五点法”画函数f（x）=Asin（ωx+
）（ω＞0，||＜
）在某一个周期内的图象时，列表并填入了部分数据，如表：
ωx+φ | 0 |
| π |
| 2π |
x |
|
| |||
Asin(ωx+φ） | 0 | 2 | -2 | 0 |
（1）请将上表数据补充完整，填写在答题卷上相应位置，并直接写出函数f（x）的解析式；
（2）若f（
）=
，求cos（2α+
）的值．
【题目】某校为了探索一种新的教学模式，进行了一项课题实验，甲班为实验班，乙班为对比班，甲乙两班的人数均为50人，一年后对两班进行测试，测试成绩的分组区间为
80,90
、90,100、100,110、110,120、120,130，由此得到两个班测试成绩的频率分布直方图：
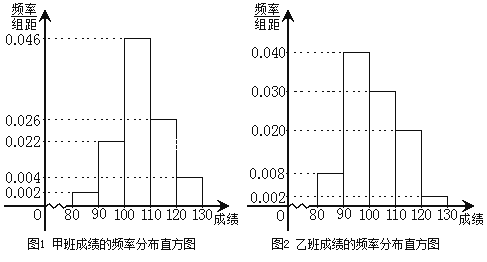
（1）完成下面2×2列联表，你能有97.5
的把握认为“这两个班在这次测试中成绩的差异与实施课题实验有关”吗？并说明理由；
成绩小于100分 | 成绩不小于100分 | 合计 | |
甲班 |
|
| 50 |
乙班 |
|
| 50 |
合计 |
|
| 100 |
（2）根据所给数据可估计在这次测试中，甲班的平均分是105.8，请你估计乙班的平均分，并计算两班平均分相差几分？
附：
，其中
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5. 024 | 6.635 | 7.879 | 10.828 |
