题目内容
【题目】已知函数![]() .
.
(1)求证:方程![]() 有实根;
有实根;
(2)![]() 在
在![]() 上是单调递减函数,求实数
上是单调递减函数,求实数![]() 的取值范围;
的取值范围;
(3)当![]() 时,关于
时,关于![]() 的不等式
的不等式![]() 的解集为空集,求所有满足条件的实数
的解集为空集,求所有满足条件的实数![]() 的值.
的值.
【答案】(1)证明见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】分析:(1)要证![]() 的实根,设
的实根,设![]() ,也就是证明方程
,也就是证明方程![]() 有非负实数根,而
有非负实数根,而![]() ,故可设
,故可设![]() 的两根为
的两根为![]() ,利用根据与系数的关系,即可求解;
,利用根据与系数的关系,即可求解;
(2)由题设值对任意的![]() 时,
时,![]() 恒成立,对
恒成立,对![]() 分类讨论,对任意的
分类讨论,对任意的![]() ,集合函数的单调性即可求出实数
,集合函数的单调性即可求出实数![]() 的取值范围;
的取值范围;
(3)由题意知,当![]() 时,
时,![]() 恒成立,记
恒成立,记![]() ,对
,对![]() 分类:若
分类:若![]() ,则
,则![]() ,从而求出满足条件的实数
,从而求出满足条件的实数![]() 的值.
的值.
详解:(1)要证x4-2ax2-1=0有实根,也就是证明方程t2-2at-1=0有非负实数根.
而Δ=4a2+4>0,故可设t2-2at-1=0的两根为t1、t2.
t1t2=-1<0,∴t1、t2一正一负.
∵方程t2-2at-1=0有正根,
∴方程f(x)=1有实根.
(2)由题设知对任意的x∈[0,1],
h′(x)=f ′(x)-1=4x3-4ax-1≤0恒成立,x=0时显然成立;
对任意的0<x≤1,a≥x2-![]() ,∴a≥(x2-
,∴a≥(x2-![]() )max,
)max,
而g(x)=x2-![]() 在(0,1]上单调递增,∴a≥g(1)=
在(0,1]上单调递增,∴a≥g(1)=![]() ,∴a的取值范围为[
,∴a的取值范围为[![]() ,+∞).
,+∞).
(3)由题设知,当x∈[0,1]时,|4x3-4ax|≤1恒成立.记F(x)=4x3-4ax,
方法1:若a≤0,则F(1)=4-4a≥4,不满足条件;
故a>0,而![]()
①当![]() <1即0<a<3时,F(x)在[0,
<1即0<a<3时,F(x)在[0,![]() ]上递减,在[
]上递减,在[![]() ,1]上递增,
,1]上递增,
于是![]() ,解得a=
,解得a=![]() .
.
②当![]() ≥1,即a≥3时,F(x)在[0,1]上递减,于是|F(x)|max=-F(1)=4a-4≥8,
≥1,即a≥3时,F(x)在[0,1]上递减,于是|F(x)|max=-F(1)=4a-4≥8,
与题意矛盾.
综上所述a=![]() .
.
方法2:(分离参数法)因为|4x3-4ax|≤1,所以-1≤4x3-4ax≤1,x=0时显然成立;
对任意的![]()
由(2)知![]() 且
且![]() 时取等号),
时取等号),![]()

 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案【题目】[2019·朝鲜中学]在如图所示的程序框图中,有这样一个执行框![]() ,其中的函数关系式为
,其中的函数关系式为![]() ,程序框图中的
,程序框图中的![]() 为函数
为函数![]() 的定义域.
的定义域.
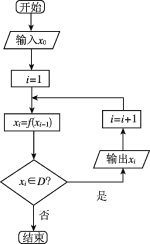
(1)若输入![]() ,请写出输出的所有
,请写出输出的所有![]() 的值;
的值;
(2)若输出的所有![]() 都相等,试求输入的初始值
都相等,试求输入的初始值![]() .
.
【题目】某校600名文科学生参加了4月25日的三调考试,学校为了了解高三文科学生的数学、外语情况,利用随机数表法从抽取100名学生的成绩进行统计分析,将学生编号为000,001,002,…599
12 56 85 99 26 96 96 68 27 31 05 03 72 93 15 57 12 10 14 21 88 26 49 81 76
55 59 56 35 64 38 54 82 46 22 31 62 43 09 90 06 18 44 32 53 23 83 01 30 30
16 22 77 94 39 49 54 43 54 82 17 37 93 23 78 87 35 20 96 43 84 26 34 91 64
84 42 17 53 31 57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76
(1)若从第6行第7列的数开始右读,请你一次写出最先抽出的5个人的编号(上面是摘自随机数表的第4行到第7行);
(2)抽出的100名学生的数学、外语成绩如下表:
外语 | ||||
优 | 良 | 及格 | ||
数学 | 优 | 8 | m | 9 |
良 | 9 | n | 11 | |
及格 | 8 | 9 | 11 | |
若数学成绩优秀率为35%,求m,n的值;
(3)在外语成绩为良的学生中,已知m≥12,n≥10,求数学成绩优比良的人数少的概率.
