题目内容
【题目】如图,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E,F,且EF=![]() , 则下列结论中错误的个数是( )
, 则下列结论中错误的个数是( )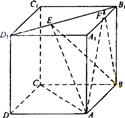
(1) AC⊥BE.
(2) 若P为AA1上的一点,则P到平面BEF的距离为![]() .
.
(3) 三棱锥A-B![]() EF的体积为定值.
EF的体积为定值.
(4) 在空间与DD1,AC,B1C1都相交的直线有无数条.
(5) 过CC1的中点与直线AC1所成角为40并且与平面BEF所成角为50的直线有2条.
A.0
B.1
C.2
D.3
【答案】A
【解析】(1)连接![]() ,由
,由![]() , 可知
, 可知![]() 面
面![]() , 而
, 而![]() 面
面![]() ,∴
,∴![]() ,(1)正确;(2)由
,(1)正确;(2)由![]() ∥面
∥面![]() , 则
, 则![]() 点到面
点到面![]() 的距离等于
的距离等于![]() 到面
到面![]() 的距离
的距离![]() , (2)正确;(3)三棱锥
, (2)正确;(3)三棱锥![]() 中,底面积是定值,高是定值,所以体积是定值,(3)正确;(4)在
中,底面积是定值,高是定值,所以体积是定值,(3)正确;(4)在![]() 上任取点
上任取点![]() , 过点
, 过点![]() 和直线
和直线![]() 确定面
确定面![]() , 设面
, 设面![]() ∩面
∩面![]() =
=![]() , 则
, 则![]() 与直线
与直线![]() 必有交点
必有交点![]() (若
(若![]() ∥
∥![]() , 则
, 则![]() ∥
∥![]() ,矛盾),则直线
,矛盾),则直线![]() 就是所画的直线,因为点
就是所画的直线,因为点![]() 的任意性,所以这样的直线有无数条,(4)正确;(5)设
的任意性,所以这样的直线有无数条,(4)正确;(5)设![]() 的中点为
的中点为![]() , 过点
, 过点![]() 与
与![]() 所成的角是
所成的角是![]() 的直线,是以与
的直线,是以与![]() 平行的直线为轴的圆锥的母线所在的直线,过点
平行的直线为轴的圆锥的母线所在的直线,过点![]() 与面
与面![]() 所成的角是
所成的角是![]() 的直线,是以过点
的直线,是以过点![]() 且与面
且与面![]() 垂直的直线为轴的 圆锥的母线,两圆锥交于两条直线,(5)正确.
垂直的直线为轴的 圆锥的母线,两圆锥交于两条直线,(5)正确.
【考点精析】本题主要考查了异面直线及其所成的角和直线与平面垂直的判定的相关知识点,需要掌握异面直线所成角的求法:1、平移法:在异面直线中的一条直线中选择一特殊点,作另一条的平行线;2、补形法:把空间图形补成熟悉的或完整的几何体,如正方体、平行六面体、长方体等,其目的在于容易发现两条异面直线间的关系;一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想才能正确解答此题.

【题目】某校为了解开展校园安全教育系列活动的成效,对全校学生进行了一次安全意识测试,根据测试成绩评定“合格”“不合格”两个等级,同时对相应等级进行量化:“合格”记5分,“不合格”记0分.现随机抽取部分学生的答卷,统计结果及对应的频率分布直方图如图所示:
等级 | 不合格 | 合格 | ||
得分 | [20,40) | [40,60) | [60,80) | [80,100] |
频数 | 6 | a | 24 | b |

(1)求a,b,c的值;
(2)先用分层抽样的方法从评定等级为“合格”和“不合格”的学生中随机抽取10人进行座谈,再从这10人中任选4人,记所选4人的量化总分为ξ,求ξ的分布列及数学期望E(ξ);
(3)某评估机构以指标![]() (
(![]() ,其中
,其中![]() 表示
表示![]() 的方差)来评估该校开展安全教育活动的成效.若
的方差)来评估该校开展安全教育活动的成效.若![]() ≥0.7,则认定教育活动是有效的;否则认定教育活动无效,应调整安全教育方案.在(2)的条件下,判断该校是否应调整安全教育方案.
≥0.7,则认定教育活动是有效的;否则认定教育活动无效,应调整安全教育方案.在(2)的条件下,判断该校是否应调整安全教育方案.




