题目内容
【题目】已知双曲线C：4x2﹣y2=4及直线l：y=kx﹣1
（1）求双曲线C的渐近线方程及离心率；
（2）直线l与双曲线C左右两支各有一个公共点，求实数k的取值范围．
【答案】
（1）解：将双曲线C：4x2﹣y2=4，化为标准方程得 
，可知焦点在x轴上，
则a=1，b=2，c= 
= 
，
∴双曲线的渐近线方程为y=± 
x=±2x，
离心率为e= 
=
（2）解：由直线l：y=kx﹣1，直线l与双曲线C相交于A，B两点，设A（x1，y1），B（x2，y2），
则 
，消去y，整理得：（4﹣k2）x2+2kx﹣5=0，
由韦达定理可知：x1x2=﹣ 
直线l与双曲线C左右两支各有一个公共点，
，
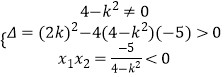解得：k2＜5，且k2＜4，
∴﹣2＜k＜2，
∴实数k的取值范围是（﹣2，2）
【解析】（1）由题意可知： 
，可知焦点在x轴上，则a=1，b=2，c= = ，渐近线方程为y=± x=±2x，离心率为e= = ；（2）将直线方程代入椭圆方程，由韦达定理可知：x1x2=﹣ ，直线l与双曲线C左右两支各有一个公共点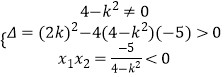， ，即可求得k的取值范围．
练习册系列答案
相关题目
