题目内容
12．
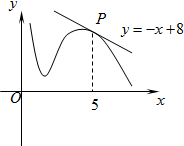如图所示，函数y=f（x）的图象在点P处的切线方程是y=-x+8，则f（5）+f′（5）=（ ）| A． | 2 | B． | 12 | C． | 8 | D． | 4 |
分析 由导数的几何意义知，函数y=f（x）的图象在点P处的切线的斜率就是函数y=f（x）在该点的导数值，因此可求得f′（5），再根据切点的双重性，即切点既在曲线上又在切线上，可求得f（5），则f（5）+f′（5）可求．
解答 解：根据图象知，函数y=f（x）的图象与在点P处的切线切于点P，
∴f（5）=-5+8=3，
又f′（5）为函数y=f（x）的图象在点P处的切线的斜率，
∴f′（5）=-1，
则f（5）+f′（5）=3-1=2．
故选：A．
点评 本题考查了利用导数研究过曲线上某点处的切线方程，过曲线上某点的切线的斜率，就是函数在该点处的导数值，是基础题．
练习册系列答案
出彩同步大试卷系列答案
相关题目
4．若曲线y=ax2在点P（1，a）处的切线与直线2x+y-6=0平行，则a=（ ）
| A． | $\frac{1}{2}$ | B． | 1 | C． | $-\frac{1}{2}$ | D． | -1 |