题目内容
17.过点(1,0)作曲线y=ex的切线,则切线方程为e2x-y-e2=0.分析 设出切点坐标(${x}_{0},{e}^{{x}_{0}}$),求出原函数的导函数,得到函数在x=x0时的导数值,即切线的斜率,然后由直线方程的点斜式得切线方程,代入已知点的坐标后求出切点的坐标,则切线方程可求.
解答 解:由线y=ex,得y′=ex,
设切点为(${x}_{0},{e}^{{x}_{0}}$),
则${y}^{′}{|}_{x={x}_{0}}={e}^{{x}_{0}}$,
∴切线方程为$y-{e}^{{x}_{0}}={e}^{{x}_{0}}(x-{x}_{0})$,
∵切线过点(1,0),
∴$-{e}^{{x}_{0}}={e}^{{x}_{0}}(1-{x}_{0})$,
解得:x0=2.
∴切线方程为y-e2=e2(x-2),整理得:e2x-y-e2=0.
故答案为:e2x-y-e2=0.
点评 本题考查了利用导数研究过曲线上某点的切线方程,过曲线上某点处的切线的斜率,就是函数在该点处的导数值,是中档题.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
12.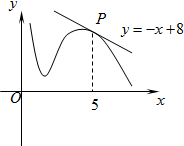 如图所示,函数y=f(x)的图象在点P处的切线方程是y=-x+8,则f(5)+f′(5)=( )
如图所示,函数y=f(x)的图象在点P处的切线方程是y=-x+8,则f(5)+f′(5)=( )
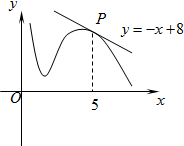 如图所示,函数y=f(x)的图象在点P处的切线方程是y=-x+8,则f(5)+f′(5)=( )
如图所示,函数y=f(x)的图象在点P处的切线方程是y=-x+8,则f(5)+f′(5)=( )| A. | 2 | B. | 12 | C. | 8 | D. | 4 |
9.已知函数f(x)=lnx-ax在点(1,f(1))处的切线平行于x轴,则a=( )
| A. | -1 | B. | -2 | C. | 1 | D. | 2 |
6.下列说法中不正确的是( )
| A. | 平面α的法向量垂直于与平面α共面的所有向量 | |
| B. | 一个平面的所有法向量互相平行 | |
| C. | 如果两个平面的法向量垂直,那么这两个平面也垂直 | |
| D. | 如果$\overrightarrow{a}$、$\overrightarrow{b}$与平面α共面且$\overrightarrow{n}$⊥$\overrightarrow{a}$,$\overrightarrow{n}$⊥$\overrightarrow{b}$,那么$\overrightarrow{n}$就是平面α的一个法向量 |
 如图,四棱锥P-ABCD的底面是正方形,PD⊥底面ABCD,点E在棱PB上
如图,四棱锥P-ABCD的底面是正方形,PD⊥底面ABCD,点E在棱PB上