题目内容
2．设O是△ABC内部一点，且$\overrightarrow{OA}$$+\overrightarrow{OC}$$+5\overrightarrow{OB}$=$\overrightarrow{0}$，则$\frac{{S}_{△AOB}}{{S}_{△AOC}}$=$\frac{4}{5}$．分析 设AC的中点为D，利用$\overrightarrow{OA}$$+\overrightarrow{OC}$$+5\overrightarrow{OB}$=$\overrightarrow{0}$，可得2$\overrightarrow{OD}$$+5\overrightarrow{OB}$=$\overrightarrow{0}$，$\frac{{S}_{△AOB}}{{S}_{△AOD}}$=$\frac{2}{5}$，从而可求$\frac{{S}_{△AOB}}{{S}_{△AOC}}$．
解答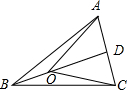 
解：设AC的中点为D，则
∵$\overrightarrow{OA}$$+\overrightarrow{OC}$$+5\overrightarrow{OB}$=$\overrightarrow{0}$，
∴2$\overrightarrow{OD}$$+5\overrightarrow{OB}$=$\overrightarrow{0}$，
∴$\frac{{S}_{△AOB}}{{S}_{△AOD}}$=$\frac{\frac{1}{2}•OB•h}{\frac{1}{2}OD•h}$=$\frac{OB}{OD}$=$\frac{2}{5}$，
∴$\frac{{S}_{△AOB}}{{S}_{△AOC}}$=$\frac{4}{5}$，
故答案为：$\frac{4}{5}$．
点评 本题考查向量在几何中的应用，考查学生的计算能力，确定2$\overrightarrow{OD}$$+5\overrightarrow{OB}$=$\overrightarrow{0}$是关键．
练习册系列答案
阅读快车系列答案
相关题目
12．
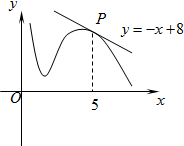如图所示，函数y=f（x）的图象在点P处的切线方程是y=-x+8，则f（5）+f′（5）=（ ）
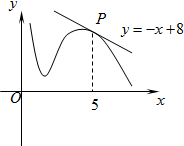如图所示，函数y=f（x）的图象在点P处的切线方程是y=-x+8，则f（5）+f′（5）=（ ）| A． | 2 | B． | 12 | C． | 8 | D． | 4 |
如图，在正四棱柱ABCD-A1B1C1D1中，AB=1，A1A=2，点E是棱CC1的中点
14．设函数f（x）的导函数为f′（x），对任意x∈R都有f（x）＞f′（x），f（x）＞0成立，若x2＞x1＞0，则（ ）
| A． | x2f（lnx1）＜x1f（lnx2） | B． | x2f（lnx1）＞x2f（lnx2） | C． | x1f（lnx1）＞x2f（lnx2） | D． | x1f（lnx1）＜x2f（lnx2） |