题目内容
设定义域为R的函数 ,若关于x的方程f2(x)+bf(x)+c=0有3个不同的整数解x1,x2,x3,则x12+x22+x32等于 .
,若关于x的方程f2(x)+bf(x)+c=0有3个不同的整数解x1,x2,x3,则x12+x22+x32等于 .
【答案】分析:根据已知中函数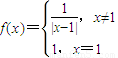 的解析式,我们可以画出函数
的解析式,我们可以画出函数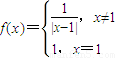 的图象,根据图象我们可以判断出关于x的方程f2(x)+bf(x)+c=0有3个不同的整数解x1,x2,x3时,x1,x2,x3的值,进而求出x12+x22+x32的值.
的图象,根据图象我们可以判断出关于x的方程f2(x)+bf(x)+c=0有3个不同的整数解x1,x2,x3时,x1,x2,x3的值,进而求出x12+x22+x32的值.
解答: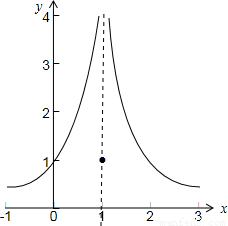 解:函数
解:函数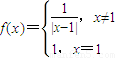 的图象如图所示:
的图象如图所示:
由图易得函数的值域为(0,+∞)
令t=f(x)
则方程f2(x)+bf(x)+c=0
可化为t2+bt+c+0,
若此方程无正根,则方程f2(x)+bf(x)+c=0无根
若此方程有一个非1的正根,则方程f2(x)+bf(x)+c=0有两根;
若此方程有一个等 1的正根,则方程f2(x)+bf(x)+c=0有三根;
此时t=f(x)=1,x1=0,x2=1,x3=2,x12+x22+x32=5
若此方程有两个非1的正根,则方程f2(x)+bf(x)+c=0有四根;
若此方程有一个非1,一个等1的正根,则方程f2(x)+bf(x)+c=0有五根;
综上x12+x22+x32=5
故答案为:5
点评:本题考查的知识点是分段函数的解析式及其图象的作法,根的存在性及根的个数判断,其中画出函数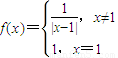 的图象,根据图象我们可以判断出关于x的方程f2(x)+bf(x)+c=0有3个不同的整数解x1,x2,x3时,所满足的条件是解答醒本题的关键.
的图象,根据图象我们可以判断出关于x的方程f2(x)+bf(x)+c=0有3个不同的整数解x1,x2,x3时,所满足的条件是解答醒本题的关键.
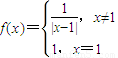 的解析式,我们可以画出函数
的解析式,我们可以画出函数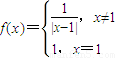 的图象,根据图象我们可以判断出关于x的方程f2(x)+bf(x)+c=0有3个不同的整数解x1,x2,x3时,x1,x2,x3的值,进而求出x12+x22+x32的值.
的图象,根据图象我们可以判断出关于x的方程f2(x)+bf(x)+c=0有3个不同的整数解x1,x2,x3时,x1,x2,x3的值,进而求出x12+x22+x32的值.解答:
 解:函数
解:函数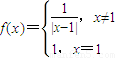 的图象如图所示:
的图象如图所示:由图易得函数的值域为(0,+∞)
令t=f(x)
则方程f2(x)+bf(x)+c=0
可化为t2+bt+c+0,
若此方程无正根,则方程f2(x)+bf(x)+c=0无根
若此方程有一个非1的正根,则方程f2(x)+bf(x)+c=0有两根;
若此方程有一个等 1的正根,则方程f2(x)+bf(x)+c=0有三根;
此时t=f(x)=1,x1=0,x2=1,x3=2,x12+x22+x32=5
若此方程有两个非1的正根,则方程f2(x)+bf(x)+c=0有四根;
若此方程有一个非1,一个等1的正根,则方程f2(x)+bf(x)+c=0有五根;
综上x12+x22+x32=5
故答案为:5
点评:本题考查的知识点是分段函数的解析式及其图象的作法,根的存在性及根的个数判断,其中画出函数
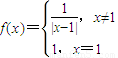 的图象,根据图象我们可以判断出关于x的方程f2(x)+bf(x)+c=0有3个不同的整数解x1,x2,x3时,所满足的条件是解答醒本题的关键.
的图象,根据图象我们可以判断出关于x的方程f2(x)+bf(x)+c=0有3个不同的整数解x1,x2,x3时,所满足的条件是解答醒本题的关键. 
练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案
相关题目
设定义域为R的函数f(x)满足下列条件:①对任意x∈R,f(x)+f(-x)=0;②对任意x1,x2∈[1,a],当x2>x1时,有f(x2)>f(x1)>0.则下列不等式不一定成立的是( )
| A、f(a)>f(0) | ||||
B、f(
| ||||
C、f(
| ||||
D、f(
|
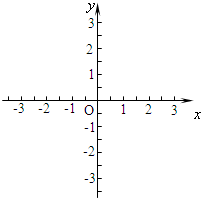 设定义域为R的函数f(x)=
设定义域为R的函数f(x)=