题目内容
【题目】已知函数![]() (
(![]() 为自然对数的底数,
为自然对数的底数,![]() ).
).
(1)求函数![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)若对于任意![]() ,存在
,存在![]() ,使得
,使得![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)若![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)对函数![]() 求导,求得
求导,求得![]() ,
,![]() ,由直线的点斜式方程可求得切线;
,由直线的点斜式方程可求得切线;
(2)对函数![]() 求导,得出函数
求导,得出函数![]() 在
在![]() 上单调性,可求得函数
上单调性,可求得函数![]() 在
在![]() 上的最值,再根据对于任意
上的最值,再根据对于任意![]() ,存在
,存在![]() ,使得
,使得![]() ,则需
,则需![]() ,
,
讨论a可求得a的范围;
(3) )因为![]() ,所以由
,所以由![]() 得
得![]() 令
令![]() ,则
,则![]() ,分析导函数的正负,得出原函数的单调性,从而得出最值,根据不等式恒成立的思想得出求得a的范围.
,分析导函数的正负,得出原函数的单调性,从而得出最值,根据不等式恒成立的思想得出求得a的范围.
(1)![]() ,
,![]() ,
,![]() ,又
,又![]() ,
,
所以切线方程为:![]() ,即
,即![]() ;
;
(2)![]() ,
,![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增,
上单调递增,![]() ,
,
由于对于任意![]() ,存在
,存在![]() ,使得
,使得![]() ,则需
,则需![]() ,
,
![]()
当![]() 时,
时,![]() ,不满足
,不满足![]() ,故
,故![]() ,
,
当![]() 时,
时,![]() 在
在![]() 上单调递增,
上单调递增,![]() ,所以
,所以![]()
![]() ,解得
,解得![]() ;
;
当![]() 时,
时,![]() 在
在![]() 上单调递减,所以
上单调递减,所以![]() 在
在![]() 上没有最大值,所以
上没有最大值,所以![]() 不满足,
不满足,
综上可得,![]() ;
;
(3)因为![]() ,所以由
,所以由![]() 得
得![]() 令
令![]() ,则
,则![]() ,
,
令![]() 则
则![]() 在
在![]() 上单调递减,且
上单调递减,且![]() ,所以存在唯一的零点
,所以存在唯一的零点![]() ,使得
,使得![]() ,
,
即有![]() 也即有
也即有![]() ,
,![]() ,即
,即![]() ,
,
所以![]() ,
,![]() ,所以
,所以![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上递减,所以
上递减,所以![]() ,
,
而![]() ,所以
,所以![]() ,
,
所以![]() .
.
所以![]() 的取值范围是
的取值范围是![]() .
.

【题目】(本题14分)下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量(![]() 吨)与相应的生产能耗
吨)与相应的生产能耗![]() (吨)标准煤的几组对照数据:
(吨)标准煤的几组对照数据:
| 3 | 4 | 5 | 6 |
| 2.5 | 3 | 4 | 4.5 |

(1)请画出上表数据的散点图;并指出x,y 是否线性相关;
(2)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)已知该厂技术改造前100吨甲产品能耗为90吨标准煤,试根据(2)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技术改造前降低多少吨标准煤?
(参考:用最小二乘法求线性回归方程系数公式 ,
,![]() )
)
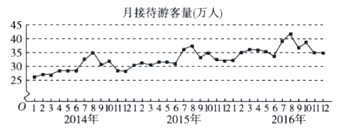
【题目】随着网络的发展,网上购物越来越受到人们的喜爱,各大购物网站为增加收入,促销策略越来越多样化,促销费用也不断增加,下表是某购物网站2018年1-8月促销费用(万元)和产品销量(万件)的具体数据:
月份 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
促销费用 | 2 | 3 | 6 | 10 | 13 | 21 | 15 | 18 |
产品销量 | 1 | 1 | 2 | 3 | 3.5 | 5 | 4 | 4.5 |
(1)根据数据绘制的散点图能够看出可用线性回归模型![]() 与
与![]() 的关系,请用相关系数
的关系,请用相关系数![]() 加以说明(系数精确到0.001);
加以说明(系数精确到0.001);
(2)建立![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() (系数精确到0.001);如果该公司计划在9月份实现产品销量超6万件,预测至少需要投入费用多少万元(结果精确到0.01).
(系数精确到0.001);如果该公司计划在9月份实现产品销量超6万件,预测至少需要投入费用多少万元(结果精确到0.01).
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,其中
,其中![]() ,
,![]() 分别为第
分别为第![]() 个月的促销费用和产品销量,
个月的促销费用和产品销量,![]() .
.
参考公式:(1)样本![]() 相关系数
相关系数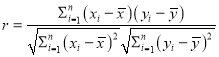 ;
;
(2)对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归方程
,其回归方程![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为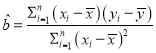 ,
,![]() .
.