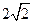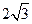题目内容
如图,已知ABCD是矩形,AB=a,AD=b,PA⊥平面ABCD,PA=2c,Q是PA的中点.
求:(1)Q到BD的距离;
(2)P到平面BQD的距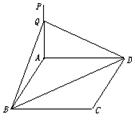
求:(1)Q到BD的距离;
(2)P到平面BQD的距

(1)Q到BD距离为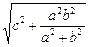 (2) P到平面BD的距离为
(2) P到平面BD的距离为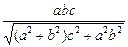
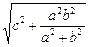 (2) P到平面BD的距离为
(2) P到平面BD的距离为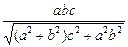
(1)在矩形ABCD中,作AE⊥BD,E为垂足
连结QE,∵QA⊥平面ABCD,由三垂线定理得QE⊥BE
∴QE的长为Q到BD的距离
在矩形ABCD中,AB=a,AD=b,
∴AE=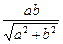
在Rt△QAE中,QA=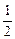 PA=c
PA=c
∴QE=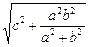
∴Q到BD距离为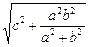
(2) ∵平面BQD经过线段PA的中点,
∴P到平面BQD的距离等于A到平面BQD的距离
在△AQE中,作AH⊥QE,H为垂足
∵BD⊥AE,BD⊥QE,∴BD⊥平面AQE ∴BD⊥AH
∴AH⊥平面BQE,即AH为A到平面BQD的距离.
在Rt△AQE中,∵AQ=c,AE=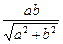
∴AH=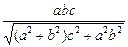
∴P到平面BD的距离为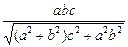
连结QE,∵QA⊥平面ABCD,由三垂线定理得QE⊥BE
∴QE的长为Q到BD的距离
在矩形ABCD中,AB=a,AD=b,
∴AE=
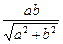
在Rt△QAE中,QA=
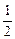 PA=c
PA=c∴QE=
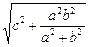
∴Q到BD距离为
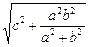
(2) ∵平面BQD经过线段PA的中点,
∴P到平面BQD的距离等于A到平面BQD的距离
在△AQE中,作AH⊥QE,H为垂足
∵BD⊥AE,BD⊥QE,∴BD⊥平面AQE ∴BD⊥AH
∴AH⊥平面BQE,即AH为A到平面BQD的距离.
在Rt△AQE中,∵AQ=c,AE=
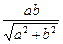
∴AH=
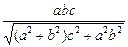
∴P到平面BD的距离为
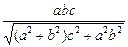

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
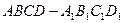 中,
中, ,点
,点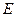 在
在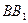 上且
上且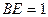 ,过点
,过点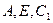 的平面截长方体,截面为
的平面截长方体,截面为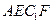 (
( 在
在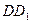 上).
上). 的长度; (2)求点C到截面
的长度; (2)求点C到截面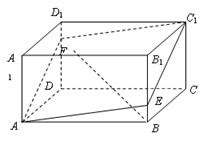
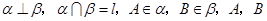 到
到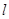 的距离分别是
的距离分别是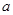 和
和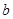 ,
,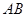 与
与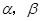 所成的角分别是
所成的角分别是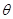 和
和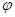 ,
,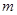 和
和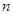 ,若
,若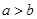 ,则( )
,则( )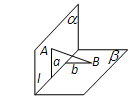
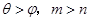
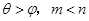
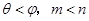
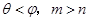
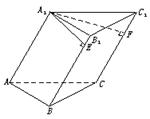
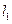 过点
过点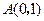 ,
,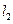 过点
过点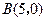 ,如果
,如果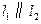 ,且
,且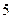 ,求
,求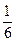 ,且满足
,且满足 则
则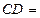 .
.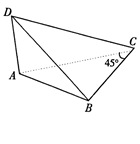

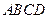 的棱长均为
的棱长均为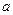 ,且
,且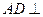 平面
平面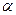 于A,点B、C、D均在平面
于A,点B、C、D均在平面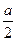 B.
B.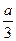 C.
C. 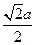 D.
D.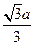
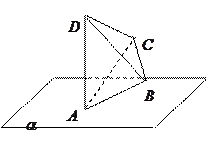
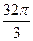 ,则OM的距离为
,则OM的距离为