题目内容
 是底面边长为1,高为2的正三棱柱被平面
是底面边长为1,高为2的正三棱柱被平面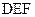 截去几何体
截去几何体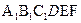 后得到的几何体,其中
后得到的几何体,其中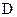 为线段
为线段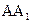 上异于
上异于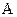 、
、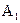 的动点,
的动点, 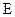 为线段
为线段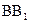 上异于
上异于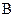 、
、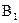 的动点,
的动点,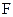 为线段
为线段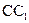 上异于
上异于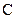 、
、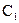 的动点,且
的动点,且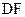 ∥
∥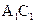 ,则下列结论中不正确的是( )
,则下列结论中不正确的是( )A.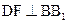 | B.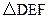 是锐角三角形 是锐角三角形 | C. 可能是棱台 可能是棱台 | D. 可能是棱柱 可能是棱柱 |
C
略

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
题目内容
 是底面边长为1,高为2的正三棱柱被平面
是底面边长为1,高为2的正三棱柱被平面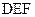 截去几何体
截去几何体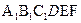 后得到的几何体,其中
后得到的几何体,其中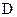 为线段
为线段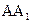 上异于
上异于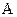 、
、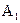 的动点,
的动点, 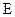 为线段
为线段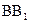 上异于
上异于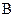 、
、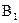 的动点,
的动点,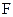 为线段
为线段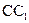 上异于
上异于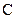 、
、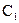 的动点,且
的动点,且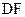 ∥
∥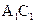 ,则下列结论中不正确的是( )
,则下列结论中不正确的是( )A.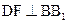 | B.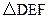 是锐角三角形 是锐角三角形 | C. 可能是棱台 可能是棱台 | D. 可能是棱柱 可能是棱柱 |

 全能测控一本好卷系列答案
全能测控一本好卷系列答案 发散思维新课堂系列答案
发散思维新课堂系列答案