题目内容
为了在夏季降温和冬季供暖时减少能源损耗,房屋的屋顶和外墙需要建造隔热层。某幢建筑物要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元。该建筑物每年的能源消耗费用C(单位:万元)与隔热层厚度x(单位:cm)满足关系:C(x)= 若不建隔热层(即x=0时),每年能源消耗费用为8万元.设f(x)为隔热层建造费用与20年的能源消耗费用之和.
若不建隔热层(即x=0时),每年能源消耗费用为8万元.设f(x)为隔热层建造费用与20年的能源消耗费用之和.
(1)求k的值;
(2)求f(x)的表达式;
(3)利用“函数 (其中
(其中 为大于0的常数),在
为大于0的常数),在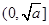 上是减函数,在
上是减函数,在 上是增函数”这一性质,求隔热层修建多厚时,总费用f(x)达到最小,并求出这个最小值.
上是增函数”这一性质,求隔热层修建多厚时,总费用f(x)达到最小,并求出这个最小值.
(1)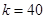 (2)f(x)=
(2)f(x)=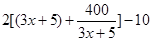 (3)隔热层修建为5厘米时,总费用最小,且最小值为70(万元)
(3)隔热层修建为5厘米时,总费用最小,且最小值为70(万元)
解析试题分析:解:(1).依题意得: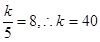 3分
3分
(2).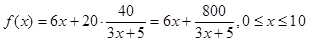 7分
7分
(3).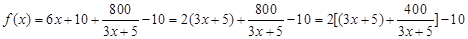 8分
8分
令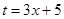 ,由
,由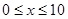 得
得 ,则
,则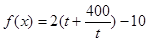 10分
10分
记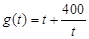 ,
,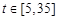 ,由性质知:函数g(t)在
,由性质知:函数g(t)在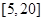 单调递减;在
单调递减;在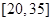
单调递增.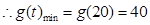 11分
11分
当t=20时,g(t)取到这个最小值.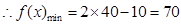 .12分
.12分
此时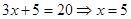 13分
13分
答:隔热层修建为5厘米时,总费用最小,且最小值为70(万元) 14分
考点:函数的最值,函数的解析式
点评:解决的关键是利用已知中的费用满足的关系式来得到,同时借助函数选项来求解最值,属于基础题。

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
已知A、B两地的路程为240千米.某经销商每天都要用汽车或火车将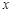 吨保鲜品一次 性由A地运往B地.受各种因素限制,下一周只能采用汽车和火车中的一种进行运输,且须提前预订.
吨保鲜品一次 性由A地运往B地.受各种因素限制,下一周只能采用汽车和火车中的一种进行运输,且须提前预订.
现有货运收费项目及收费标准表、行驶路程s(千米)与行驶时间t(时)的函数图象(如图1)、上周货运量折线统计图(如图2)等信息如下:
货运收费项目及收费标准表
| 运输工具 | 运输费单价:元/(吨•千米) | 冷藏费单价:元/(吨•时) | 固定费用:元/次 |
| 汽车 | 2 | 5 | 200 |
| 火车 | 1.6 | 5 | 2280 |
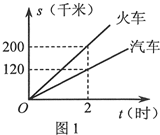
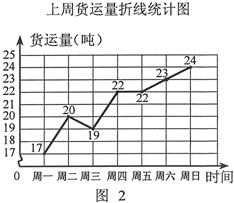
(1)汽车的速度为 千米/时,火车的速度为 千米/时:
(2)设每天用汽车和火车运输的总费用分别为
 汽(元)和
汽(元)和 火(元),分别求
火(元),分别求 汽、
汽、 火与
火与 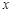 的函数关系式(不必写出
的函数关系式(不必写出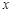 的取值范围),及
的取值范围),及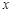 为何值时
为何值时 汽>
汽> 火(总费用=运输费+冷藏费+固定费用)
火(总费用=运输费+冷藏费+固定费用)(3)请你从平均数、折线图走势两个角度分析,建议该经销商应提前为下周预定哪种运输工具,才能使每天的运输总费用较省?
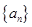 的前n项和
的前n项和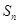
 m2,为了使堤的上面与两侧面的水泥用料最省,要求断面的外周长(梯形的上底BC与两腰长的和)最小.如何设计防洪堤,才能使水泥用料最省.
m2,为了使堤的上面与两侧面的水泥用料最省,要求断面的外周长(梯形的上底BC与两腰长的和)最小.如何设计防洪堤,才能使水泥用料最省.
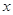 元.
元.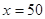 时,凌霄同学将在毕业后第几个月还清最后一笔贷款?他当月工资余额能否满足当月3000元的基本生活费?(6分)
时,凌霄同学将在毕业后第几个月还清最后一笔贷款?他当月工资余额能否满足当月3000元的基本生活费?(6分)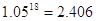 ,
,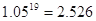 ,
,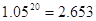 ,
, 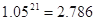 )
) ,在
,在 时取得极值.
时取得极值. 的解析式;
的解析式; 时,
时, 恒成立,求实数m的取值范围;
恒成立,求实数m的取值范围; ,是否存在实数b,使得方程
,是否存在实数b,使得方程 在区间
在区间 上恰有两个相异实数根,若存在,求出b的范围,若不存在说明理由.
上恰有两个相异实数根,若存在,求出b的范围,若不存在说明理由.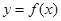 的图象.写出
的图象.写出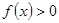 的解集;
的解集;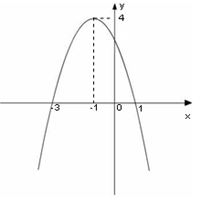
 在何范围内变化时,
在何范围内变化时,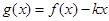 在区间
在区间 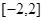 上是单调函数.
上是单调函数.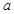 元(
元(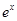 (e为自然对数的底数)成反比例。已知每件产品的日售价为40元时,日销售量为10件。
(e为自然对数的底数)成反比例。已知每件产品的日售价为40元时,日销售量为10件。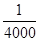 ).假设所有的列车长度l均为0.4千米,最大速度均为v0(千米/小时).问:列车车速多大时,单位时间流量Q=
).假设所有的列车长度l均为0.4千米,最大速度均为v0(千米/小时).问:列车车速多大时,单位时间流量Q=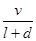 最大?
最大?