题目内容
设抛物线C:y2=4x的焦点为F,直线l过F且与C交于A,B两点.若|AF|=3|BF|,则l的方程为( )
| A.y=x-1或y=-x+1 |
B.y= (x-1)或y=- (x-1)或y=- (x-1) (x-1) |
C.y= (x-1)或y=- (x-1)或y=- (x-1) (x-1) |
D.y= (x-1)或y=- (x-1)或y=- (x-1) (x-1) |
C
设A(x1,y1),B(x2,y2),
又F(1,0),
则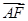 =(1-x1,-y1),
=(1-x1,-y1),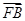 =(x2-1,y2),
=(x2-1,y2),
由题意知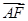 =3
=3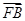 ,
,
因此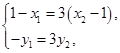
即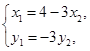
又由A、B均在抛物线上知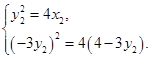
解得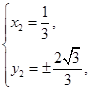
直线l的斜率为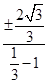 =±
=± ,
,
因此直线l的方程为y= (x-1)或y=-
(x-1)或y=- (x-1).
(x-1).
故选C.
又F(1,0),
则
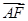 =(1-x1,-y1),
=(1-x1,-y1),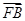 =(x2-1,y2),
=(x2-1,y2),由题意知
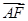 =3
=3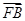 ,
,因此
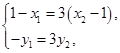
即
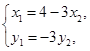
又由A、B均在抛物线上知
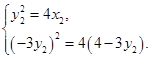
解得
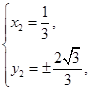
直线l的斜率为
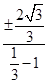 =±
=± ,
,因此直线l的方程为y=
 (x-1)或y=-
(x-1)或y=- (x-1).
(x-1).故选C.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
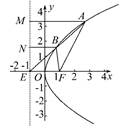
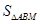 的最大值
的最大值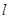 时,拱顶离水面2米,水面宽4米,水位下降1米后,水面宽 米.
时,拱顶离水面2米,水面宽4米,水位下降1米后,水面宽 米.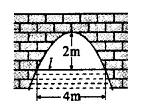
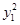 +
+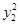 的最小值是( )
的最小值是( )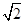 时,切线MA的斜率为-
时,切线MA的斜率为-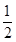 .
.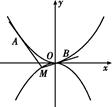
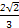
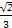


 的焦点为
的焦点为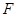 ,顶点为
,顶点为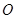 ,准线为
,准线为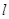 ,过该抛物线上异于顶点
,过该抛物线上异于顶点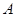 作
作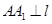 于点
于点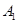 ,以线段
,以线段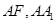 为邻边作平行四边形
为邻边作平行四边形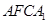 ,连接直线
,连接直线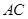 交
交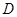 ,延长
,延长 交抛物线于另一点
交抛物线于另一点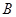 .若
.若 的面积为
的面积为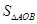 ,
,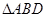 的面积为
的面积为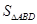 ,则
,则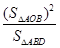 的最大值为____________.
的最大值为____________.