题目内容
15.已知函数f(x)=lnx+$\frac{m}{x}$(1)当函数f(x)在点(1,f(1))处的切线与直线4y-x+1=0垂直时,求实数m的值.
(2)若x≥1时,f(x)≥1恒成立,求实数m的取值范围.
分析 (1)可求导数,f′(x)=$\frac{1}{x}-\frac{m}{{x}^{2}}$,从而可以求出f(x)在点x=1处的切线斜率k=f′(1),而根据切线和直线4y-x+1=0垂直,这样便知切线斜率为-4,从而有f′(1)=-4,这样即可求出m的值;
(2)由条件便可得到m≥x-xlnx在x≥1上恒成立,可设g(x)=x-xlnx,并求得g′(x)=-lnx,从而可说明g′(x)≤0,从而得出g(x)在[1,+∞)上单调递减,从而可求出g(x)在[1,+∞)上的最大值,从而便可得出实数m的取值范围.
解答 解:(1)$f′(x)=\frac{1}{x}-\frac{m}{{x}^{2}}$;
切线和直线4y-x+1=0垂直;
∴切线斜率为-4;
∴f′(1)=1-m=-4;
∴m=5;
(2)x≥1时,f(x)≥1恒成立;
∴$lnx+\frac{m}{x}≥1$恒成立;
∴m≥x-xlnx在x≥1上恒成立,设g(x)=x-xlnx,g′(x)=-lnx;
x≥1;
∴-lnx≤0;
∴g(x)在x≥1上单调递减;
∴g(x)在x≥1上的最大值为g(1)=1;
∴m≥1;
∴实数m的取值范围为:[1,+∞).
点评 考查函数在图象上某点的导数和过该点的切线斜率的关系,根据导数符号判断函数单调性的关系,根据函数的单调性求函数的最值,掌握恒成立问题的解法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.已知函数f(x)=ax3+bx2-3x(a,b∈R),在点(1,f(1))处的切线方程为y+2=0.若对于区间[-2,2]上任意两个自变量的值x1,x2,都有|f(x1)-f(x2)|≤c,则实数c的取值范围是( )
| A. | c≥4 | B. | c≥3 | C. | c≥2 | D. | c≥1 |
7.已知定义在实数解R上的函数f(x)满足f(1)=2,且f(x)的导函数f′(x)在R上恒有f′(x)<1,则不等式f(x)<x+1的解集为( )
| A. | (-1,1) | B. | (-∞,-1) | C. | (1,+∞) | D. | (-∞,-1)∪(1,+∞) |
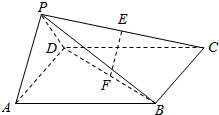 如图,在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,侧面PAD⊥底面ABCD,且PA=PD=$\frac{{\sqrt{2}}}{2}$AD,E、F分别为PC、BD的中点.
如图,在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,侧面PAD⊥底面ABCD,且PA=PD=$\frac{{\sqrt{2}}}{2}$AD,E、F分别为PC、BD的中点.