题目内容
3.已知数列{an}满足a1=1,an+1=pan+q,且a2=3,a4=15,则p+q=3.分析 由已知条件利用递推公式推导出a2和a4关于p,q的方程,解方程组能求出p,q的值,由此能求出p+q.
解答 解:∵数列{an}满足a1=1,an+1=pan+q,且a2=3,a4=15,
∴a2=pa1+q,即p+q=3,
${a}_{4}=p{a}_{3}+q=p(p{a}_{2}+q)+q={p}^{2}{a}_{2}+pq+q$,
即3p2+pq+q=15,
联立$\left\{\begin{array}{l}{p+q=3}\\{3{p}^{2}+pq+q=15}\end{array}\right.$,
解得$\left\{\begin{array}{l}{p=-3}\\{q=6}\end{array}\right.$或$\left\{\begin{array}{l}{p=2}\\{q=1}\end{array}\right.$,
∴p+q=-3+6=3或p+q=1+2=3.
故答案为:3.
点评 本题考查p+q的值的求法,是中档题,解题时要认真审题,注意递推公式的合理运用.

练习册系列答案
相关题目
18.设函数y=f(x)定义域为{x|x∈R且x≠1},已知f(x+1)为奇函数,当x<1时,f(x)=2x2-x+1,则x>1时,f(x)的递减区间为( )
| A. | [$\frac{5}{4}$,+∞) | B. | (1,$\frac{5}{4}$] | C. | [$\frac{7}{4}$,+∞) | D. | (1,$\frac{7}{4}$] |
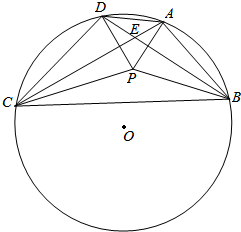 凸四边形ABCD的外接圆的圆心O,已知AC≠BD,AC与BD交于点E,若P为四边形ABCD内部一点,使得∠PAB+∠PCB=∠PBC+∠PDC=90°,求证:O,P,E三点共线.
凸四边形ABCD的外接圆的圆心O,已知AC≠BD,AC与BD交于点E,若P为四边形ABCD内部一点,使得∠PAB+∠PCB=∠PBC+∠PDC=90°,求证:O,P,E三点共线.