题目内容
20.已知函数f(x)=ax3+bx2-3x(a,b∈R),在点(1,f(1))处的切线方程为y+2=0.若对于区间[-2,2]上任意两个自变量的值x1,x2,都有|f(x1)-f(x2)|≤c,则实数c的取值范围是( )| A. | c≥4 | B. | c≥3 | C. | c≥2 | D. | c≥1 |
分析 求出函数的导数,由题意可得f(1)=-2,f′(1)=0,解方程可得a=1,b=0,进而得到f(x)的解析式,求得导数,求得极值和端点的函数值,得到[-2,2]上的最值,即可得到c的范围.
解答 解:f(x)的导数为f′(x)=3ax2+2bx-3,
根据题意,得$\left\{\begin{array}{l}{f(1)=a+b-3=-2}\\{f′(1)=3a+2b-3=0}\end{array}\right.$
解得$\left\{\begin{array}{l}{a=1}\\{b=0}\end{array}\right.$,则f(x)=x3-3x,
令f′(x)=3x2-3=0,解得x=±1,
由f(-1)=2,f(1)=-2,f(-2)=-2,f(2)=2,
当x∈[-2,2]时,f(x)min=-2,f(x)max=2,
由|f(x1)-f(x2)|≤|f(x)max-f(x)min|=4,
可得c≥4,
故选:A.
点评 本题考查导数的运用:求切线的斜率和单调区间、极值和最值,同时考查不等式恒成立思想的运用,属于中档题.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目
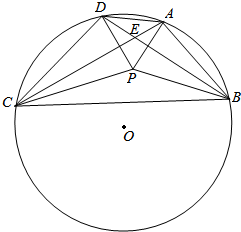 凸四边形ABCD的外接圆的圆心O,已知AC≠BD,AC与BD交于点E,若P为四边形ABCD内部一点,使得∠PAB+∠PCB=∠PBC+∠PDC=90°,求证:O,P,E三点共线.
凸四边形ABCD的外接圆的圆心O,已知AC≠BD,AC与BD交于点E,若P为四边形ABCD内部一点,使得∠PAB+∠PCB=∠PBC+∠PDC=90°,求证:O,P,E三点共线. 如图,四面体ABCS中,SA,SB,SC两两垂直,∠ABS=45°,∠ABC=60°,M为AB的中点.
如图,四面体ABCS中,SA,SB,SC两两垂直,∠ABS=45°,∠ABC=60°,M为AB的中点.