题目内容
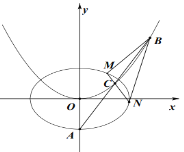
【题目】如图,![]() 为椭圆
为椭圆![]() 的下顶点.过
的下顶点.过![]() 的直线
的直线![]() 交抛物线
交抛物线![]() 于
于![]() ,
,![]() 两点,
两点,![]() 是
是![]() 的中点.
的中点.
(1)求证:点![]() 的纵坐标是定值;
的纵坐标是定值;
(2)过点![]() 作与直线
作与直线![]() 倾斜角互补的直线
倾斜角互补的直线![]() 交椭圆于
交椭圆于![]() ,
,![]() 两点.求
两点.求![]() 的值,使得
的值,使得![]() 的面积最大.
的面积最大.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)由题意可求![]() ,设
,设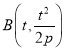 ,利用
,利用![]() 是
是![]() 的中点,求出
的中点,求出![]() 的坐标,代入抛物线方程,可得
的坐标,代入抛物线方程,可得![]() 的关系,再代入点
的关系,再代入点![]() 的纵坐标即可得出结果;
的纵坐标即可得出结果;
(2)由题意可得![]() ,进而可以表示出直线
,进而可以表示出直线![]() 的斜率和直线
的斜率和直线![]() 斜率,则可求出直线
斜率,则可求出直线![]() 的方程,与椭圆方程联立,利用韦达定理,求出
的方程,与椭圆方程联立,利用韦达定理,求出![]() 的长和点
的长和点![]() 到
到![]() 的距离,
的距离,
从而可以求出![]() ,变形,利用基本不等式求其最值,通过等号的成立条件可求出
,变形,利用基本不等式求其最值,通过等号的成立条件可求出![]() 的值.
的值.
(1)易知![]() ,不妨设
,不妨设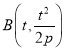 ,则
,则 ,代入抛物线方程得:
,代入抛物线方程得:
![]() ,得:
,得:![]() ,∴
,∴![]() 为定值.
为定值.
(2)∵点![]() 是
是![]() 中点,∴
中点,∴![]() ,
,
∵直线![]() 的斜率
的斜率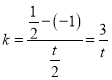 ,直线
,直线![]() 斜率
斜率![]() ,
,
∴直线![]() 的方程:
的方程:![]() ,即
,即![]() ,不妨记
,不妨记![]() ,则
,则![]() :
:![]() ,
,
代入椭圆方程整理得:![]() ,设
,设![]() ,
,![]() ,则
,则
![]() ,
,![]() ,
,
![]() ,
,
![]() 到
到![]() 的距离
的距离![]() ,
,
所以![]()
![]()
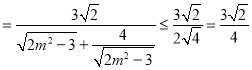 .
.
取等号时,![]() ,得
,得![]() ,
,
所以![]() ,
,![]() .
.

 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案【题目】为了解少年儿童的肥胖是否与常喝碳酸饮料有关,现对![]() 名小学六年级学生进行了问卷调查,并得到如下列联表.平均每天喝
名小学六年级学生进行了问卷调查,并得到如下列联表.平均每天喝![]() 以上为“常喝”,体重超过
以上为“常喝”,体重超过![]() 为“肥胖”.
为“肥胖”.
常喝 | 不常喝 | 合计 | |
肥胖 | 2 | ||
不肥胖 | 18 | ||
合计 | 30 |
已知在全部![]() 人中随机抽取
人中随机抽取![]() 人,抽到肥胖的学生的概率为
人,抽到肥胖的学生的概率为![]() .
.
(1)请将上面的列联表补充完整;
(2)是否有![]() 的把握认为肥胖与常喝碳酸饮料有关?请说明你的理由;
的把握认为肥胖与常喝碳酸饮料有关?请说明你的理由;
(3)已知常喝碳酸饮料且肥胖的学生中恰有2名女生,现从常喝碳酸饮料且肥胖的学生中随机抽取2人参加一个有关健康饮食的电视节目,求恰好抽到一名男生和一名女生的概率.
附:![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
【题目】为了引导居民合理用水,某市决定全面实施阶梯水价.阶梯水价原则上以住宅(一套住宅为一户)的月用水量为基准定价,具体划分标准如表:
阶梯级别 | 第一阶梯水量 | 第二阶梯水量 | 第三阶梯水量 |
月用水量范围(单位:立方米) |
|
|
|
从本市随机抽取了10户家庭,统计了同一月份的月用水量,得到如图茎叶图:

(1)现要在这10户家庭中任意选取3家,求取到第二阶梯水量的户数![]() 的分布列与数学期望;
的分布列与数学期望;
(2)用抽到的10户家庭作为样本估计全市的居民用水情况,从全市依次随机抽取10户,若抽到![]() 户月用水量为二阶的可能性最大,求
户月用水量为二阶的可能性最大,求![]() 的值.
的值.
