题目内容
已知函数![]() .
.
(Ⅰ) 若![]() ,且
,且![]() 存在单调递减区间,求
存在单调递减区间,求![]() 的取值范围;
的取值范围;
(Ⅱ) 若函数![]() 的图像与
的图像与![]() 轴交于A,B两点,线段AB中点的横坐标为
轴交于A,B两点,线段AB中点的横坐标为![]() ,证明:
,证明:![]() .
.
解:(I)当![]() 时,
时,![]()
则![]() …………………………………………2
…………………………………………2
因为函数![]() 存在单调递减区间,所以
存在单调递减区间,所以![]() <0有解.
<0有解.
又因为x>0时,则ax2+2x-1>0有x>0的解.
①当a>0时,y=ax2+2x-1为开口向上的抛物线,ax2+2x-1>0总有x>0的解;
②当a<0时,y=ax2+2x-1为开口向下的抛物线,若ax2+2x-1>0总有x>0的解;
则需△=4+4a>0,且方程ax2+2x-1=0至少有一正根.此时,-1<a<0.
综上所述,a的取值范围为(-1,0)∪(0,+∞). ……………………5
(II) 设点A,B的坐标分别是(x1, 0),(x2, 0),0<x1<x2.
则点AB的中点横坐标为![]()
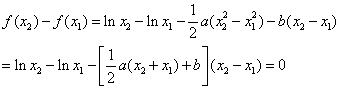
则 ![]() …………………………………………7
…………………………………………7
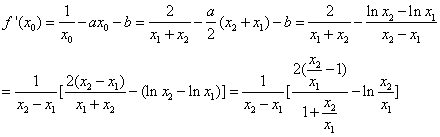 ……………………9
……………………9
设![]() 则
则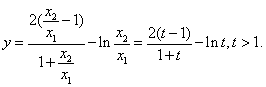
令![]() 则
则![]()
因为![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() )上单调递减. 故
)上单调递减. 故![]()
而![]() . 故
. 故![]() …………………………………………12
…………………………………………12

练习册系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(
| ||||
B、f(x)=2sin(
| ||||
C、f(x)=2sin(2x-
| ||||
D、f(x)=2sin(2x+
|