题目内容
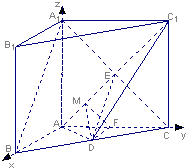
如图,在三棱柱A
1B
1C
1-ABC中,A
1A⊥平面ABC,A
1A=AB=AC,AB⊥AC,点D是BC上一点,且AD⊥C
1D.
(1)求证:平面ADC
1⊥平面BCC
1B
1;
(2)求证:A
1B
∥平面ADC
1;
(3)求二面角C-AC
1-D大小的余弦值.

(1)证明:依题意,C
1C⊥平面ABC,∵AD?平面ABC∴C
1C⊥AD,…(2分)
又AD⊥C
1D,∴C
1C∩C
1D=C
1∴AD⊥平面BC
1,又AD?平面ABC…(3分)
∴平面ADC
1⊥平面BCC
1B
1…(4分)
(2)证明:连接A
1C交AC
1于点E,则E是A
1C的中点,连接DE.…(5分)
由(1)知AD⊥平面BC
1,∴AD⊥BC,∴D是BC中点…(6分)
∴A
1B
∥DE…(7分)
又∵DE?平面ADC
1,∵A
1B?平面ADC
1∴A
1B
∥平面ADC
1.…(8分)
(3)如图,建立空间直角坐标系Axyz,设A
1A=AB=AC=2,
则A(0,0,0),D(1,1,0),C
1(0,2,2).…(9分)
=(1,1,0),
=(0,2,2),
设平面ADC
1的一个法向量为
=(x,y,z),
则
•=0,•=0,
即
,令x=1,得y=-1,z=1,
∴
=(1,-1,1).
取平面CAC
1的一个法向量为
=(1,0,0),…(11分)
则
cos<,>===.
所以二面角C-AC
1-D大小的余弦值为
.…(13分)
练习册系列答案
相关题目










 中,
中, ,
, 为
为 的中点,且
的中点,且 ,则
,则 .
.