题目内容
已知a＞b＞0，全集U=R，集合M={x|b＜x＜
}，N={x|
＜x＜a}，P={x|b＜x≤}，则P，M，N满足的关系是
- A.P=M∪N
- B.P=M∩N
- C.P=M∩（CUN）
- D.P=（CUM）∩N
C
分析：由已知a＞b＞0，可得
，再结合数轴即可得出答案．
解答：∵a＞b＞0，∴．
∵N={x|＜x＜a}，全集U=R，画出数轴可知，∴CUN={x|x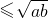
，x≥a}，
又M={x|b＜x＜}，
∴M∩（CUN）={x|b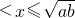
}，
又∵P={x|b＜x≤}，∴M∩（CUN）=P．
故选C．
点评：本题考查了集合的运算，正确理解集合的运算法则和基本不等式及数形结合是vjk解决问题的关键．
分析：由已知a＞b＞0，可得
，再结合数轴即可得出答案．解答：∵a＞b＞0，∴
．∵N={x|
＜x＜a}，全集U=R，画出数轴可知，∴CUN={x|x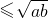，x≥a}，又M={x|b＜x＜
}，∴M∩（CUN）={x|b
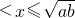}，又∵P={x|b＜x≤
}，∴M∩（CUN）=P．故选C．
点评：本题考查了集合的运算，正确理解集合的运算法则和基本不等式及数形结合是vjk解决问题的关键．
练习册系列答案
巧学巧练系列答案
相关题目
已知a＞b＞0，全集为R，集合E={x|b＜x＜
}，F={x|
＜x＜a}，M={x|b＜x≤
}，则有（ ）
| a+b |
| 2 |
| ab |
| ab |
| A、M=E∩（CRF） |
| B、M=（CRE）∩F |
| C、M=E∪F |
| D、M=E∩F |
已知a＞b＞0，全集U=R，M={x|b＜x＜
}，N={x|
＜x＜a}，P={x|b＜x≤
}，则（ ）
| ab |
|
|
| A、P=M∩（CUN） |
| B、P=（CUM）∩N |
| C、P=M∩N |
| D、P=M∪N |