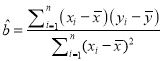题目内容
【题目】已知![]() .
.
(Ⅰ)当![]() 时,求
时,求![]() 的极值;
的极值;
(Ⅱ)若![]() 有2个不同零点,求
有2个不同零点,求![]() 的取值范围;
的取值范围;
(Ⅲ)对![]() ,求证:
,求证: ![]() .
.
【答案】(1) ![]() ,无极大值(2)
,无极大值(2) ![]() (3)见解析
(3)见解析
【解析】试题分析:(Ⅰ)求导,利用导函数的符号确定函数的单调性,进而确定函数的极值;(Ⅱ)求导,讨论![]() 的取值,研究导函数的符号变换,得到函数单调性和极值,再通过零点的个数确定极值的符号;(Ⅲ)作差构造函数,求导,利用导数求其最值即可证明.
的取值,研究导函数的符号变换,得到函数单调性和极值,再通过零点的个数确定极值的符号;(Ⅲ)作差构造函数,求导,利用导数求其最值即可证明.
试题解析:(Ⅰ)当![]() 时
时 ![]()
![]() ,
, ![]() ,
, ![]() 为减函数
为减函数
![]() ,
, ![]() ,
, ![]() 为增函数
为增函数
∴![]() ,无极大值;
,无极大值;
(Ⅱ)![]()
![]() 当
当![]() 时,
时, ![]() ,只有个零点
,只有个零点![]()
![]() 当
当![]() 时,
时, ![]()
![]() ,
, ![]() ,
, ![]() 为减函数
为减函数
![]() ,
, ![]() ,
, ![]() 为增函数
为增函数
![]() 而
而![]()
∴当![]() ,
, ![]() ,使
,使![]()
当![]() 时,∴
时,∴![]() ∴
∴![]()
∴![]()
![]()
取![]() ,∴
,∴![]()
![]()
∴函数有![]() 个零点
个零点
![]() 当
当![]() 时,
时, ![]()
令![]() 得
得![]() ,
, ![]()
①![]() ,即
,即![]() 时
时
当![]() 变化时
变化时 ![]() ,
, ![]() 变化情况是
变化情况是
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
∴![]()
∴函数![]() 至多有一个零点,不符合题意
至多有一个零点,不符合题意
②![]() 时,
时, ![]() ,
, ![]() 在
在![]() 单调递增
单调递增
∴![]() 至多有一个零点,不合题意
至多有一个零点,不合题意
③当![]() 时,即以
时,即以![]() 时
时
当![]() 变化时
变化时![]() ,
, ![]() 的变化情况是
的变化情况是
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∴![]() ,
, ![]() 时
时
![]()
![]()
∴函数![]() 至多有个零点
至多有个零点
综上: ![]() 的取值范围是
的取值范围是![]()
(Ⅲ)令![]()
![]()
![]()
![]()
![]()
令![]() 行禁止
行禁止 ![]()
![]() ∴
∴![]() 为增函数
为增函数
![]()
取![]() ,
, ![]() ,
, ![]()
∴存在唯一![]() 使
使![]() ,即
,即![]()
![]() ,
, ![]() ,即
,即![]() ,∴
,∴![]() 为减函数
为减函数
![]() ,
, ![]() ,即
,即![]() ,∴
,∴![]() 为增函数
为增函数
∴![]()
![]()
![]()
![]()
∴对![]() 有
有![]()
即![]()

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目