题目内容
设集合 ,那么“m
,那么“m A”是“m
A”是“m B”的
B”的
| A.充要条件 | B.必要而不充分条件 |
| C.充分而不必要条件 | D.既不充分也不必要条件 |
C
解析试题分析: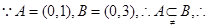 “m
“m A”是“m
A”是“m B”的充分而不必要条件.
B”的充分而不必要条件.
考点:考查了分式不等式的解法,集合之间的包含关系,充要条件等内容.
点评:根据集合间的包含关系来确定是哪种充要关系是解本小题的基本思路.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
下列特称命题中假命题的个数是()
①有的实数是无限不循环小数②有些三角形不是等腰三角形③有的菱形是正方形
| A.0 | B.1 | C.2 | D.3 |
已知 ,那么“
,那么“ ”是 “
”是 “ ”的( )
”的( )
| A.充要条件 | B.充分不必要条件 |
| C.必要不充分条件 | D.既不充分也不必要条件 |
设 ,则“
,则“ ”是“直线
”是“直线 与直线
与直线 平行的( )
平行的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
下列命题正确的是( )
A.已知 ,则 ,则 |
B.存在实数 ,使 ,使 成立 成立 |
C.命题 对任意的 对任意的 ,则 ,则 :对任意的 :对任意的 |
| D.若p或q为假命题,则p,q均为假命题 |
下列命题是真命题的是
①“若 ,则
,则 不全为零”的否命题;
不全为零”的否命题;
②“正六边形都相似”的逆命题;
③“若 ,则
,则 有实根”的逆否命题;
有实根”的逆否命题;
④“若 是有理数,则
是有理数,则 是无理数”.
是无理数”.
| A.①④ | B.③④ | C.①③④ | D.①②③④ |
命题“函数 是奇函数”的否定是( )
是奇函数”的否定是( )
A. , , | B. , ,  |
C. , , | D. , , |
下列判断错误的是( )
| A.a,b,m为实数,则“am2<bm2”是“a<b”的充分不必要条件 |
B.对于命题 : :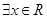 ,命题 ,命题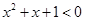 ,则 ,则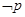 为: 为: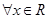 ,均有 ,均有 |
| C.若p∧q为假命题,则p,q均为假命题 |
D.命题“若 ,则 ,则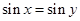 ”的逆否命题为真命题 ”的逆否命题为真命题 |
 ,则“
,则“ ”是 “
”是 “ ”的( )
”的( )