题目内容
下列命题是真命题的是
①“若 ,则
,则 不全为零”的否命题;
不全为零”的否命题;
②“正六边形都相似”的逆命题;
③“若 ,则
,则 有实根”的逆否命题;
有实根”的逆否命题;
④“若 是有理数,则
是有理数,则 是无理数”.
是无理数”.
| A.①④ | B.③④ | C.①③④ | D.①②③④ |
C
解析试题分析:因为选项①“若 ,则
,则 不全为零”的否命题为;“若
不全为零”的否命题为;“若 ,则
,则 全为零,那么根据方程的性质可知,平方和为零,必然都为零,可知x,y都是零故其否命题正确。而②“正六边形都相似”的逆命题是两相似的六边形是正六边形,不成立。故命题为假。③“若
全为零,那么根据方程的性质可知,平方和为零,必然都为零,可知x,y都是零故其否命题正确。而②“正六边形都相似”的逆命题是两相似的六边形是正六边形,不成立。故命题为假。③“若 ,则
,则 有实根”的逆否命题的真值就是原命题的真值,因为
有实根”的逆否命题的真值就是原命题的真值,因为 有实根,则说明判别式大于等于零,即1+4m
有实根,则说明判别式大于等于零,即1+4m ,而命题中的条件是
,而命题中的条件是 ,利用集合思想可知,小集合是大集合的充分不必要条件,故命题正确。而④“若
,利用集合思想可知,小集合是大集合的充分不必要条件,故命题正确。而④“若 是有理数,则
是有理数,则 是无理数”,中
是无理数”,中 是无理数,无理数与无理数相减才可以为有理数,因此成立。故选C
是无理数,无理数与无理数相减才可以为有理数,因此成立。故选C
考点:本试题主要考查了命题真假的判定问题,以及四种命题的表述和判定。
点评:解决该试题的关键是对于条件和结论的否定是否正确。

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
下列命题正确的是( )
A. | B. |
C. 是 是 的充分不必要条件 的充分不必要条件 | D.若 ,则 ,则 |
下列结论中,正确的是( )
①命题“如果 ,则
,则 ”的逆否命题是“如果
”的逆否命题是“如果 ,则
,则 ”;
”;
②已知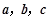 为非零的平面向量.甲:
为非零的平面向量.甲: ,乙:
,乙: ,则甲是乙的必要条件,但不是充分条件;
,则甲是乙的必要条件,但不是充分条件;
③ 是周期函数,
是周期函数, 是周期函数,则
是周期函数,则 是真命题;
是真命题;
④命题 的否定是:
的否定是: .
.
| A.①② | B.①④ | C.①②④ | D.①③④ |
设集合 ,那么“m
,那么“m A”是“m
A”是“m B”的
B”的
| A.充要条件 | B.必要而不充分条件 |
| C.充分而不必要条件 | D.既不充分也不必要条件 |
已知命题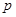 :
: ,则( )
,则( )
A.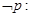 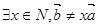 | B.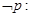  |
C.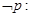 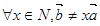 | D.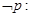  |
已知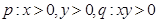 ,则p是q的( )
,则p是q的( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
已知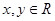 ,则“
,则“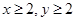 ”是“
”是“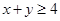 ”成立的( )
”成立的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
“ ”是“方程
”是“方程 至少有一个负根”的
至少有一个负根”的
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分又不必要条件 |
 ”是“命题
”是“命题 ”成立的必要不充分条件,则实数
”成立的必要不充分条件,则实数 的取值范围为 ( )
的取值范围为 ( )


