题目内容
设 ,则“
,则“ ”是“直线
”是“直线 与直线
与直线 平行的( )
平行的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
A
解析试题分析:由于“ ”是“直线
”是“直线 与直线
与直线 ,可知满足平行关系,因为A,B相同,C不同,结合一般式中斜率和截距的关系判定得到。
,可知满足平行关系,因为A,B相同,C不同,结合一般式中斜率和截距的关系判定得到。
当 “直线 与直线
与直线 平行时,那么根据充要条件得到为2-a(a+1)=0,a=1,a=-2,截距不同,那么根据第一条直线过原点截距都为零,第二条直线的横
平行时,那么根据充要条件得到为2-a(a+1)=0,a=1,a=-2,截距不同,那么根据第一条直线过原点截距都为零,第二条直线的横
截距不为零,说明平行。显然可知条件能推出结论,结论不能推出条件,因此为选项A.
考点:本试题主要考查了两条直线平行的充要条件的运用。
点评:解决该试题的关键是对于两直线平行要考虑斜率存在时和斜率不存在时两种情况来得到结论。

练习册系列答案
相关题目
“m=4”是“直线(m+2)x+2my-1=0与直线(m+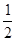 )x+(m+2)y+3=0相互平行”的
)x+(m+2)y+3=0相互平行”的
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要 |
命题“对任意的 ”的否定是( )
”的否定是( )
A.不存在 | B.存在 |
C.存在 | D.对任意的 |
下列结论中,正确的是( )
①命题“如果 ,则
,则 ”的逆否命题是“如果
”的逆否命题是“如果 ,则
,则 ”;
”;
②已知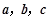 为非零的平面向量.甲:
为非零的平面向量.甲: ,乙:
,乙: ,则甲是乙的必要条件,但不是充分条件;
,则甲是乙的必要条件,但不是充分条件;
③ 是周期函数,
是周期函数, 是周期函数,则
是周期函数,则 是真命题;
是真命题;
④命题 的否定是:
的否定是: .
.
| A.①② | B.①④ | C.①②④ | D.①③④ |
有下列四个命题:①“若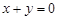 ,则
,则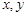 互为相反数”的逆命题;②“全等三角形的面积相等”的否命题;③“若
互为相反数”的逆命题;②“全等三角形的面积相等”的否命题;③“若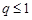 ,则
,则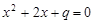 有实根”的逆命题;④“不等边三角形的三个内角相等”的逆否命题;其中真命题有( )
有实根”的逆命题;④“不等边三角形的三个内角相等”的逆否命题;其中真命题有( )
| A.①② | B.②③ | C.①③ | D.③④ |
设集合 ,那么“m
,那么“m A”是“m
A”是“m B”的
B”的
| A.充要条件 | B.必要而不充分条件 |
| C.充分而不必要条件 | D.既不充分也不必要条件 |
已知命题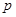 :
: ,则( )
,则( )
A.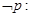 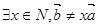 | B.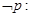  |
C.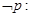 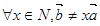 | D.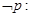  |
已知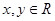 ,则“
,则“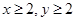 ”是“
”是“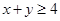 ”成立的( )
”成立的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
“ ”是“
”是“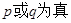 ”的( )
”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |