题目内容
已知 ,则“
,则“ ”是 “
”是 “ ”的( )
”的( )
A.充分不必要条件
B 必要不充分条件
C. 充要条件
D. 既不充分也不必要条件
A
解析试题分析:因为由已知, 在其定义域内递增函数,所以a,b>0那么可知a>b>0;而对于
在其定义域内递增函数,所以a,b>0那么可知a>b>0;而对于 在R上递减的,那么可知a>b,所以说条件和结论表示的集合之间,前者小,后者大,利用集合的思想可知道,前者是后者成立的充分不必要条件,故选A.
在R上递减的,那么可知a>b,所以说条件和结论表示的集合之间,前者小,后者大,利用集合的思想可知道,前者是后者成立的充分不必要条件,故选A.
考点:本试题主要考查了对数函数与指数函数单调性的运用,和充分条件的判定问题综合应用。
点评:解决该试题的关键是能利用对数函数但单调性确定真数的大小关系,然后结合指数函数的单调性进而判定大小。

练习册系列答案
相关题目
若“ ,
, ”为真命题,则实数
”为真命题,则实数 的取值范围是( )
的取值范围是( )
A. | B.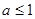 | C. | D. |
在实数集 中,我们定义的大小关系“
中,我们定义的大小关系“ ”为全体实数排了一个“序”,类似地,我们在复数集
”为全体实数排了一个“序”,类似地,我们在复数集 上也可以定义一个称为“序”的关系,记为“
上也可以定义一个称为“序”的关系,记为“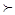 ”。定义如下:对于任意两个复数
”。定义如下:对于任意两个复数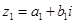 ,
, (
( ,
, 为虚数单位),“
为虚数单位),“ ”当且仅当“
”当且仅当“ ”或“
”或“ 且
且 ”.下面命题为假命题的是( )
”.下面命题为假命题的是( )
A.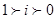 |
B.若 , , ,则 ,则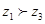 |
C.若 ,则对于任意 ,则对于任意 , ,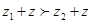 |
D.对于复数 ,若 ,若 ,则 ,则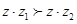 |
若 ,则“
,则“ ”是“
”是“ ”的( ) 条件
”的( ) 条件
| A.充分而不必要 | B.必要而不充分 |
| C.充要 | D.既不充分又不必要 |
下列结论中,正确的是( )
①命题“如果 ,则
,则 ”的逆否命题是“如果
”的逆否命题是“如果 ,则
,则 ”;
”;
②已知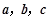 为非零的平面向量.甲:
为非零的平面向量.甲: ,乙:
,乙: ,则甲是乙的必要条件,但不是充分条件;
,则甲是乙的必要条件,但不是充分条件;
③ 是周期函数,
是周期函数, 是周期函数,则
是周期函数,则 是真命题;
是真命题;
④命题 的否定是:
的否定是: .
.
| A.①② | B.①④ | C.①②④ | D.①③④ |
对于常数 、
、 ,“
,“ ”是“方程
”是“方程 的曲线是椭圆”的( )
的曲线是椭圆”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
设集合 ,那么“m
,那么“m A”是“m
A”是“m B”的
B”的
| A.充要条件 | B.必要而不充分条件 |
| C.充分而不必要条件 | D.既不充分也不必要条件 |
已知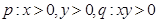 ,则p是q的( )
,则p是q的( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
下列命题中,真命题是( )
A.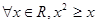 | B.命题“若 ”的逆命题 ”的逆命题 |
C.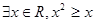 | D.命题“若 ”的逆否命题 ”的逆否命题 |