题目内容
已知数列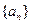 和
和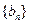 满足
满足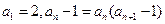 ,
,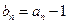 ,
,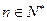 .
.
(1)求数列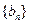 的通项公式;
的通项公式;
(2)设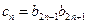 ,求使得
,求使得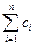
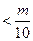 对一切
对一切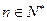 都成立的最小正整数
都成立的最小正整数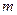 ;
;
(3)设数列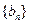 的前
的前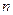 和为
和为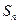 ,
,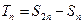 ,试比较
,试比较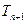 与
与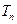 的大小.
的大小.
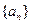 和
和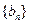 满足
满足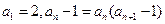 ,
,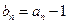 ,
,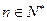 .
.(1)求数列
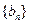 的通项公式;
的通项公式;(2)设
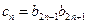 ,求使得
,求使得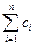
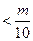 对一切
对一切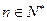 都成立的最小正整数
都成立的最小正整数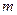 ;
;(3)设数列
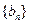 的前
的前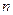 和为
和为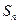 ,
,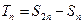 ,试比较
,试比较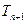 与
与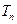 的大小.
的大小.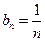 ,满足要求的最小正整数
,满足要求的最小正整数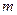 为5,
为5,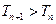
解:(1)由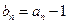 得
得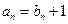 代入
代入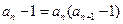 得
得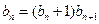 ,
,
整理得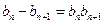 ,---------------------------------------------------------------2分
,---------------------------------------------------------------2分
∵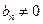 否则
否则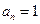 ,与
,与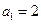 矛盾,从而得
矛盾,从而得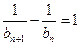 , -----------------------------4分
, -----------------------------4分
∵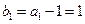 ∴数列
∴数列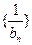 是首项为1,公差为1的等差数列
是首项为1,公差为1的等差数列
∴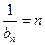 ,即
,即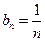 .------------------------------------------------------------------------5分
.------------------------------------------------------------------------5分
(2)∵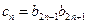 =
=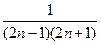 =
=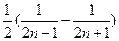 --------------------------6分
--------------------------6分
∴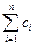 =
=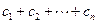 =
=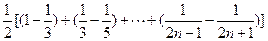 =
=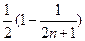 --8分
--8分
∴要使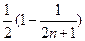
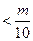 对一切
对一切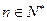 都成立,必须并且只须满足
都成立,必须并且只须满足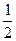 ≤
≤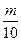 ,即m≥5,
,即m≥5,
∴满足要求的最小正整数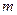 为5.-----------------------------------------------------------10分
为5.-----------------------------------------------------------10分
(3)∵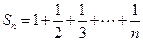
∴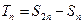 =
=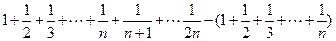
=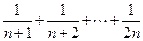 -------------------------------------------------------------12分
-------------------------------------------------------------12分
又∵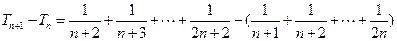
=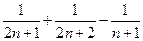 =
=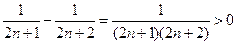
∴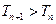 .--------------------------------------------------------------------------------14分
.--------------------------------------------------------------------------------14分
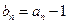 得
得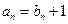 代入
代入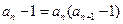 得
得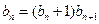 ,
,整理得
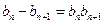 ,---------------------------------------------------------------2分
,---------------------------------------------------------------2分∵
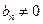 否则
否则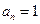 ,与
,与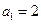 矛盾,从而得
矛盾,从而得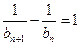 , -----------------------------4分
, -----------------------------4分∵
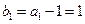 ∴数列
∴数列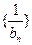 是首项为1,公差为1的等差数列
是首项为1,公差为1的等差数列∴
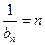 ,即
,即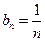 .------------------------------------------------------------------------5分
.------------------------------------------------------------------------5分(2)∵
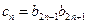 =
=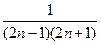 =
=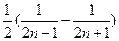 --------------------------6分
--------------------------6分∴
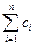 =
=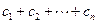 =
=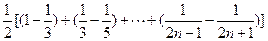 =
=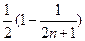 --8分
--8分∴要使
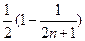
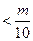 对一切
对一切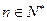 都成立,必须并且只须满足
都成立,必须并且只须满足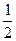 ≤
≤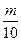 ,即m≥5,
,即m≥5,∴满足要求的最小正整数
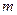 为5.-----------------------------------------------------------10分
为5.-----------------------------------------------------------10分(3)∵
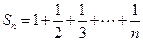
∴
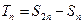 =
=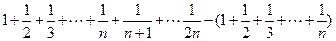
=
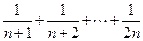 -------------------------------------------------------------12分
-------------------------------------------------------------12分又∵
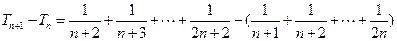
=
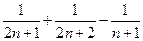 =
=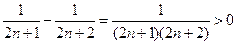
∴
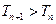 .--------------------------------------------------------------------------------14分
.--------------------------------------------------------------------------------14分
练习册系列答案
相关题目
 的前
的前 项和记为
项和记为
 的各项为正,其前
的各项为正,其前 ,且
,且 ,又
,又 成等比数列,求
成等比数列,求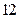 分)设数列
分)设数列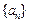 的前
的前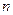 项和为
项和为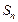 ,且
,且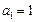 ,
,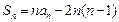 .
.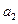 ,
,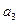 ,
,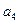 ,并求出数列
,并求出数列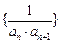 的前
的前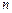 项和为
项和为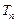 ,试求
,试求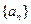 的前
的前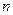 项和为
项和为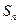 ,对一切
,对一切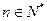 ,点
,点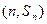 在函数
在函数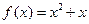 的图象上.
的图象上.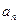 的表达式;
的表达式;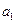 ),(
),(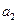 ,
,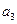 ),(
),(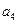 ,
,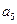 ,
,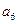 ),(
),(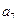 ,
,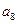 ,
,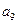 ,
,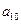 );(
);(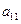 ),(
),(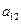 ,
,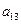 ),(
),(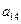 ,
,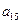 ,
,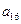 ),(
),(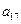 ,
,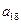 ,
,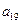 ,
,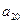 );(
);(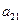 ),…,分别计算各个括号内所有项之和,并设由这些和按原来括号的前后顺序构成的数列为
),…,分别计算各个括号内所有项之和,并设由这些和按原来括号的前后顺序构成的数列为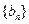 ,求
,求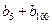 的值;
的值;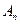 为数列
为数列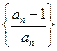 的前
的前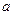 ,使得不等式
,使得不等式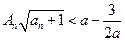 对一切
对一切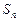 为等差数列
为等差数列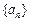 的前
的前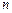 项和,且
项和,且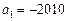 ,
,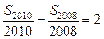 ,则
,则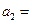 ( )
( )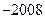
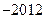
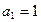 ,
,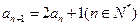 ,则
,则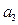 的值为
的值为 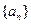 的前n项和为
的前n项和为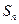 ,若
,若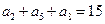 , 则
, 则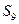 =
= ( ).
( ).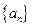 中,
中,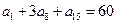 ,则
,则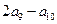 的值为
的值为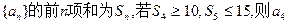 的最大值是 。
的最大值是 。