题目内容

【题目】已知λ∈R，函数 g（x）=x2﹣4x+1+4λ，若关于x的方程f（g（x））=λ有6个解，则λ的取值范围为（ ）
A.
B.
C.
D.

【答案】D
【解析】解：令g（x）=t，则方程f（t）=λ的解有3个，由图象可得，0＜λ＜1．
且三个解分别为t1=﹣1﹣λ，t2=﹣1+λ，t3=10λ ，
则x2﹣4x+1+4λ=﹣1﹣λ，x2﹣4x+1+4λ=﹣1+λ，
x2﹣4x+1+4λ=10λ ， 均有两个不相等的实根，
则△1＞0，且△2＞0，且△3＞0，
即16﹣4（2+5λ）＞0且16﹣4（2+3λ）＞0，解得0＜λ＜ ，
当0＜λ＜ 时，△3=16﹣4（1+4λ﹣10λ）＞0即3﹣4λ+10λ＞0恒成立，
故λ的取值范围为（0， ）．
故选D．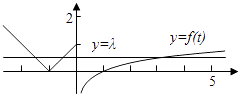

练习册系列答案
相关题目

【题目】如图，四面体中， 平面， ， ， ， .

（Ⅰ）求四面体的四个面的面积中，最大的面积是多少？

（Ⅱ）证明：在线段上存在点，使得，并求的值．

【题目】已知f（x）是定义在[1，+∞]上的函数，且f（x）= ，则函数y=2xf（x）﹣3在区间（1，2015）上零点的个数为 ．

【题目】已知条件p：A={x|x2﹣2mx+m2﹣4≤0，x∈R，m∈R}，条件q：B={x|x2﹣2x﹣3≤0，x∈R}．
（1）若A∩B={x|0≤x≤3}，求实数m的值；
（2）若q是￢p的充分条件，求实数m的取值范围．

【题目】从椭圆上一点向轴作垂线，垂足恰好为椭圆的左焦点， 是椭圆的右顶点， 是椭圆的上顶点，且.

（1）求该椭圆的方程；

（2）不过原点的直线与椭圆交于两点，已知，直线， 的斜率, 成等比数列，记以， 为直径的圆的面积分别为，求证； 为定值，并求出定值.

【题目】已知直线l1：(a－1)x＋y＋b＝0，l2：ax＋by－4＝0，求满足下列条件的a，b的值．

(1)l1⊥l2，且l1过点(1,1)；

(2)l1∥l2，且l2在第一象限内与两坐标轴围成的三角形的面积为2.

【题目】已知椭圆： 的左、右焦点分别为，离心率， 为椭圆上的任意一点（不含长轴端点），且面积的最大值为1.

（1）求椭圆的方程；

（2）已知直线与椭圆交于不同的两点，且线段的中点不在圆内，求的取值范围.

【题目】某市电视台为了宣传举办问答活动，随机对该市15～65岁的人群抽样了人，回答问题计结果如下图表所示：

（1）分别求出的值；

（2）从第2，3，4组回答正确的人中用分层抽样的方法抽取6人，则第2，3，4组每组各抽取多少人？

（3）在（2）的前提下，电视台决定在所抽取的6人中随机抽取2人颁发幸运奖，求所抽取的人中第2组至少有1人获得幸运奖的概率.

【题目】如图1所示，在边长为4的菱形ABCD中，∠DAB=60°，点E，F分别是边CD，CB的中点，EF∩AC=O，沿EF将△CEF翻折到△PEF，连接PA，PB，PD，得到如图2所示五棱锥P﹣ABFED，且AP= ，
（1）求证：BD⊥平面POA；
（2）求二面角B﹣AP﹣O的正切值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网