题目内容
【题目】已知函数f(x)![]() x2﹣(6+a)x+2alnx(a∈R).
x2﹣(6+a)x+2alnx(a∈R).
(1)讨论f(x)的单调性;
(2)函数g(x)![]() x2+(2a﹣4)lnx﹣1,若存在x0∈[1,e],使得f(x0)<g(x0)成立,求a的取值范围.
x2+(2a﹣4)lnx﹣1,若存在x0∈[1,e],使得f(x0)<g(x0)成立,求a的取值范围.
【答案】(1) 当a>6时,f(x)在(![]() ,+∞),(0,2)上单调递增,在(2,
,+∞),(0,2)上单调递增,在(2,![]() )上单调递减.
)上单调递减.
当a=6时,f(x)在(0,+∞)上单调递增.
当0<a<6时,f(x)在(2,+∞),(0,![]() )上单调递增,f(x)在(
)上单调递增,f(x)在(![]() ,2)上单调递减.
,2)上单调递减.
当a≤0时,f(x)在(2,+∞)上单调递增.
(2) (﹣5,+∞).
【解析】
(1)首先对f(x)求导数,令![]() ,再讨论当
,再讨论当![]() 、a=6、
、a=6、![]() 、
、![]() 四种情况对应的单调性。
四种情况对应的单调性。
(2)首先由f(x)<g(x),化简得4lnx+1<(6+a)x,因为x∈[1,e],所以a>[![]() ]min,
]min,
令h(x)![]() ,对 h(x)求导判断其单调性即可。求出最小值即可。
,对 h(x)求导判断其单调性即可。求出最小值即可。
(1)f′(x)=3x﹣(6+a)![]() (x>0),
(x>0),
令f′(x)=0,得x1![]() ,x2=2,
,x2=2,
①当![]() 及a>6时,
及a>6时,
若x∈(![]() ,+∞)∪(0,2),f′(x)>0,故f(x)在(
,+∞)∪(0,2),f′(x)>0,故f(x)在(![]() ,+∞),(0,2)上单调递增,
,+∞),(0,2)上单调递增,
若x∈(2,![]() ),f′(x)<0,故f(x)在(2,
),f′(x)<0,故f(x)在(2,![]() )上单调递减.
)上单调递减.
②当a=6时,f′(x)≥0对x∈(0,+∞)恒成立,
故f(x)在(0,+∞)上单调递增.
③当0![]() 2,即0<a<6时,
2,即0<a<6时,
若x∈(2,+∞)∪(0,![]() ),f′(x)>0,故f(x)在(2,+∞),(0,
),f′(x)>0,故f(x)在(2,+∞),(0,![]() )上单调递增
)上单调递增
若x∈(![]() ,2),f′(x)<0,故f(x)在(
,2),f′(x)<0,故f(x)在(![]() ,2)上单调递减.
,2)上单调递减.
④当![]() ,即a≤0时,
,即a≤0时,
若x∈(2,+∞),f′(x)>0,故f(x)在(2,+∞)上单调递增,
若x∈(0,2),f′(x)<0,f(x)在(0,2)单调递减.
综上所述:当a>6时,f(x)在(![]() ,+∞),(0,2)上单调递增,在(2,
,+∞),(0,2)上单调递增,在(2,![]() )上单调递减.
)上单调递减.
当a=6时,f(x)在(0,+∞)上单调递增.
当0<a<6时,f(x)在(2,+∞),(0,![]() )上单调递增,f(x)在(
)上单调递增,f(x)在(![]() ,2)上单调递减.
,2)上单调递减.
当a≤0时,f(x)在(2,+∞)上单调递增.
(2)当x∈[1,e],由f(x)<g(x),化简得4lnx+1<(6+a)x,
因为x∈[1,e],所以a>[![]() ]min,
]min,
令h(x)![]() ,
,![]() ,
,
令h′(x)=0,得x=e![]() ,
,
当x∈[1,e![]() )时,h′(x)>0,h(x)单调递增.
)时,h′(x)>0,h(x)单调递增.
当x∈(e![]() ,e]时,h′(x)<0,h(x)单调递减.
,e]时,h′(x)<0,h(x)单调递减.
所以h(x)min={h(1),h(e)},
h(1)=﹣5<h(e)![]() ,
,
所以a>﹣5,
故a的取值范围是(﹣5,+∞).

 科学实验活动册系列答案
科学实验活动册系列答案【题目】党的十九大明确把精准脱贫作为决胜全面建成小康社会必须打好的三大攻坚战之一.为坚决打赢脱贫攻坚战,某帮扶单位为帮助定点扶贫村脱贫,坚持扶贫同扶智相结合,此帮扶单位考察了甲、乙两种不同的农产品加工生产方式,现对两种生产方式的产品质量进行对比,其质量按测试指标可划分为:指标在区间![]() 的为优等品;指标在区间
的为优等品;指标在区间![]() 的为合格品,现分别从甲、乙两种不同加工方式生产的农产品中,各自随机抽取100件作为样本进行检测,测试指标结果的频数分布表如下:
的为合格品,现分别从甲、乙两种不同加工方式生产的农产品中,各自随机抽取100件作为样本进行检测,测试指标结果的频数分布表如下:
甲种生产方式:
指标区间 |
|
|
|
|
|
|
频数 | 5 | 15 | 20 | 30 | 15 | 15 |
乙种生产方式:
指标区间 |
|
|
|
|
|
|
频数 | 5 | 15 | 20 | 30 | 20 | 10 |
(1)在用甲种方式生产的产品中,按合格品与优等品用分层抽样方式,随机抽出5件产品,①求这5件产品中,优等品和合格品各多少件;②再从这5件产品中,随机抽出2件,求这2件中恰有1件是优等品的概率;
(2)所加工生产的农产品,若是优等品每件可售55元,若是合格品每件可售25元.甲种生产方式每生产一件产品的成本为15元,乙种生产方式每生产一件产品的成本为20元.用样本估计总体比较在甲、乙两种不同生产方式下,该扶贫单位要选择哪种生产方式来帮助该扶贫村来脱贫?
【题目】某校抽取了100名学生期中考试的英语和数学成绩,已知成绩都不低于100分,其中英语成绩的频率分布直方图如图所示,成绩分组区间是![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
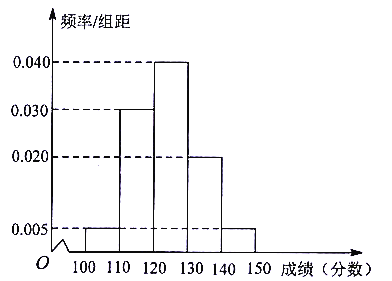
(1)根据频率分布直方图,估计这100名学生英语成绩的平均数和中位数(同一组数据用该区间的中点值作代表);
(2)若这100名学生数学成绩分数段的人数y的情况如下表所示:
分组区间 |
|
|
|
|
|
y | 15 | 40 | 40 | m | n |
且区间![]() 内英语人数与数学人数之比为
内英语人数与数学人数之比为![]() ,现从数学成绩在
,现从数学成绩在![]() 的学生中随机选取2人,求选出的2人中恰好有1人数学成绩在
的学生中随机选取2人,求选出的2人中恰好有1人数学成绩在![]() 的概率.
的概率.