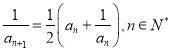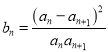Question

【题目】解答
（1）设复数z满足|z|=1，且（3+4i）z为纯虚数，求 ；
（2）已知（2 ﹣ ）n的展开式中所有二项式系数之和为64，求展开式的常数项．

Answer 1

【答案】
（1）解：设z=a+bi，则依题意得（3+4i）（a+bi）=3a﹣4b+（3b+4a）i为纯虚数，且|z|=1，

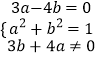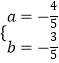∴ ，解之得 或 ，

∴ 或

（2）解：依题意得2n=64，∴n=6．

展开式中第r+1项为 = ，

当3﹣r=0时，即r=3，

∴

【解析】（1）设z=a+bi，则依题意得（3+4i）（a+bi）=3a﹣4b+（3b+4a）i为纯虚数，且|z|=1，列出方程组，求解即可得答案；（2）利用二项式定理系数的性质，求出n，然后通过二项式定理的通项公式求出常数项即可．
【考点精析】掌握复数的乘法与除法是解答本题的根本，需要知道设则；．