题目内容
9.函数f(x)=log2(1-$\frac{1}{x}$)的定义域为(-∞,0)∪(1,+∞).分析 根据对数函数的性质得到关于x的不等式,解出即可.
解答 解:由题意得:
1-$\frac{1}{x}$>0,解得:x>1或x<0,
故答案为:(-∞,0)∪(1,+∞).
点评 本题考查了函数的定义域问题,考查对数函数的性质,是一道基础题.

练习册系列答案
相关题目
14.直线y=1被椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{2}$=1截得的线段长为( )
| A. | 4$\sqrt{2}$ | B. | 3$\sqrt{2}$ | C. | 2$\sqrt{2}$ | D. | $\sqrt{2}$ |
18.设函数f(x)=$\left\{\begin{array}{l}{2-x,0≤x≤1}\\{(x-2)^{2},1<x≤2}\end{array}\right.$,则f[f($\frac{3}{2}$)]的值等于( )
| A. | $\frac{3}{4}$ | B. | $\frac{5}{4}$ | C. | $\frac{7}{4}$ | D. | $\frac{9}{4}$ |
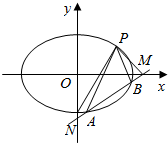 如图,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1的离心率为$\frac{{\sqrt{3}}}{2}$,过椭圆C上一点P(2,1)作倾斜角互补的两条直线,分别与椭圆交于点A、B,直线AB与x轴交于点M,与y轴负半轴交于点N.
如图,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1的离心率为$\frac{{\sqrt{3}}}{2}$,过椭圆C上一点P(2,1)作倾斜角互补的两条直线,分别与椭圆交于点A、B,直线AB与x轴交于点M,与y轴负半轴交于点N.