题目内容
(1)一种产品的年产量原来是a件,在今后m年内,计划使年产量平均每年比上一年增加p%,写出年产量随经过年数变化的函数关系式.
(2)一种产品的成本原来是a元,在今后m年内,计划使成本平均每年比上一年降低p%,写出成本随经过年数变化的函数关系式.
解:(1)设年产量经过x年增加到y件,
第一年为 y=a(1+p%)
第二年为 y=a(1+p%)(1+p%)=a(1+p%)2
第三年为 y=a(1+p%)(1+p%)(1+p%)=a(1+p%)3
…
则y=a(1+p%)x(x∈N*且x≤m).
(2)设成本经过x年降低到y元,
第一年为 y=a(1-p%)
第二年为 y=a(1-p%)(1-p%)=a(1-p%)2
第三年为 y=a(1-p%)(1-p%)(1-p%)=a(1-p%)3
…
则y=a(1-p%)x(x∈N*且x≤m).
分析:(1)年产量平均每年比上一年增加p%,可以先算出第一年产量是 y=a(1+p%),依此类推,找出规律,可以算出年产量随经过年数变化的函数关系;
(2)年产量平均每年比上一年减少p%,可以先算出第一年产量是 y=a(1-p%),依此类推,找出规律,可以算出年产量随经过年数变化的函数关系.
点评:增长率问题是一重要的模型.本题主要考查建立函数关系,用数学知识解决实际问题的能力.
第一年为 y=a(1+p%)
第二年为 y=a(1+p%)(1+p%)=a(1+p%)2
第三年为 y=a(1+p%)(1+p%)(1+p%)=a(1+p%)3
…
则y=a(1+p%)x(x∈N*且x≤m).
(2)设成本经过x年降低到y元,
第一年为 y=a(1-p%)
第二年为 y=a(1-p%)(1-p%)=a(1-p%)2
第三年为 y=a(1-p%)(1-p%)(1-p%)=a(1-p%)3
…
则y=a(1-p%)x(x∈N*且x≤m).
分析:(1)年产量平均每年比上一年增加p%,可以先算出第一年产量是 y=a(1+p%),依此类推,找出规律,可以算出年产量随经过年数变化的函数关系;
(2)年产量平均每年比上一年减少p%,可以先算出第一年产量是 y=a(1-p%),依此类推,找出规律,可以算出年产量随经过年数变化的函数关系.
点评:增长率问题是一重要的模型.本题主要考查建立函数关系,用数学知识解决实际问题的能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 对于如图的立体图形,则它的侧视图是
对于如图的立体图形,则它的侧视图是

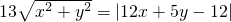 ,则动点M的轨迹是
,则动点M的轨迹是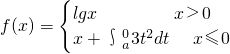 ,若f(f(1))=1,则a=________.
,若f(f(1))=1,则a=________.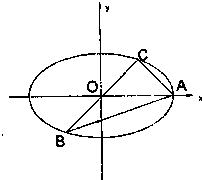 如图,已知A、B、C是长轴为4的椭圆上的三点,点A是长轴的右顶点,BC过椭圆中心O,且
如图,已知A、B、C是长轴为4的椭圆上的三点,点A是长轴的右顶点,BC过椭圆中心O,且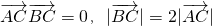 ,
,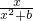 ,其中b∈R.
,其中b∈R. ,
, ],使f(x)≥1,求b的取值范围.
],使f(x)≥1,求b的取值范围.