题目内容
【题目】如图,在同一平面内,点P位于两平行直线l1、l2两侧,且P到l1 , l2的距离分别为1,3,点M,N分别在l1 , l2上,| ![]() +
+ ![]() |=8,则
|=8,则 ![]()
![]() 的最大值为( )
的最大值为( ) 
A.15
B.12
C.10
D.9
【答案】A
【解析】解:由点P位于两平行直线l1 , l2的同侧,且A到l1 , l2的距离分别为1,3, 可得平行线l1、l2间的距离为2;
以直线l2为x轴,以过点P且与直线l2垂直的直线为y轴,
建立坐标系,如图所示:
由题意可得点P(0,﹣1),直线l1的方程为y=2,
设点M(a,0)、点N(b,2),
∴ ![]() =(a,1)、
=(a,1)、 ![]() =(b,3),
=(b,3),
∴ ![]() +
+ ![]() =(a+b,4);
=(a+b,4);
∵| ![]() +
+ ![]() |=8,
|=8,
∴(a+b)2+16=64,
∴a+b=4 ![]() ,或a+b=﹣4
,或a+b=﹣4 ![]() ;
;
当a+b=4 ![]() 时,
时, ![]()
![]() =ab+3=a(4
=ab+3=a(4 ![]() ﹣a)+3=﹣a2+4
﹣a)+3=﹣a2+4 ![]() a+3,
a+3,
它的最大值为﹣ ![]() +4
+4 ![]() ×2
×2 ![]() +3=15;
+3=15;
当a+b=﹣3时, ![]() =ab+3=a(﹣4
=ab+3=a(﹣4 ![]() ﹣a)+3=﹣a2﹣4
﹣a)+3=﹣a2﹣4 ![]() a+3,
a+3,
它的最大值为﹣ ![]() ﹣4
﹣4 ![]() ×(﹣2
×(﹣2 ![]() )+3=15;
)+3=15;
综上可得, ![]() 的最大值为15.
的最大值为15.
故选:A.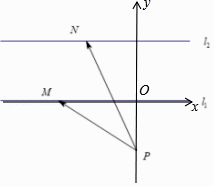

【题目】为了解春季昼夜温差大小与某种子发芽多少之间的关系,现在从4月份的30天中随机挑选了5天进行研究,且分别记录了每天昼夜温差与每天每100颗种子浸泡后的发芽数,得到如下表格:
日期 | 4月1日 | 4月7日 | 4月15日 | 4月21日 | 4月30日 |
温差x/℃ | 10 | 11 | 13 | 12 | 8 |
发芽数y/颗 | 23 | 25 | 30 | 26 | 16 |
(1)从这5天中任选2天,记发芽的种子数分别为![]() ,求事件“
,求事件“![]() 均不小于25”的概率;
均不小于25”的概率;
(2) 若由线性回归方程得到的估计数据与4月份所选5天的检验数据的误差均不超过2颗,则认为得到的线性回归方程是可靠的. 请根据4月7日,4月15日与4月21日这三天的数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并判定所得的线性回归方程是否可靠?
,并判定所得的线性回归方程是否可靠?
参考公式:  ,
, ![]()
参考数据: ![]()

