题目内容
【题目】已知各项均为正数的数列![]() 的首项
的首项![]() ,
, ![]() 是数列
是数列![]() 的前
的前![]() 项和,且满足:
项和,且满足:
![]() .
.
(1)若![]() 成等比数列,求实数
成等比数列,求实数![]() 的值;
的值;
(2)若![]() ,求证:数列
,求证:数列 为等差数列;
为等差数列;
(3)在(2)的条件下,求![]() .
.
【答案】(1)1;(2)证明见解析;(3) ![]() .
.
【解析】试题分析:(1)在题中等式中分号令n=1,2,3,解出![]() (用
(用![]() 表示),利用
表示),利用![]() 解得
解得![]() 。(2)由于要证数列
。(2)由于要证数列 为等差数列,所以要构出相除的形式,只需把题中等式两边同时除以
为等差数列,所以要构出相除的形式,只需把题中等式两边同时除以![]() ,即可证。(3)由(2)
,即可证。(3)由(2)![]() .再由
.再由![]() ,解得
,解得![]() ,代入上式中可得
,代入上式中可得![]() 。
。
试题解析:(1)令![]() ,得
,得![]()
令![]() ,得
,得![]() ,所以
,所以![]()
由![]() ,得
,得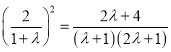 ,因为
,因为![]() ,所以
,所以![]() .
.
(2)当![]() 时,
时, ![]() ,
,
所以![]() ,即
,即![]()
所以数列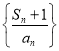 是以2为首项,公差为
是以2为首项,公差为![]() 的等差数列,
的等差数列,
所以![]() ,即
,即![]() .
.
(3)![]() ,①
,①
当![]() 时,
时, ![]() ,②
,②
①-②得, ![]()
即![]() ,所以
,所以![]() ,
,
所以![]() 是首项为
是首项为![]() 的常数列,所以
的常数列,所以![]() ,
,
代入①得![]() .
.

【题目】某职称晋级评定机构对参加某次专业技术考试的100人的成绩进行了统计,绘制了频率分布直方图(如图所示).规定80分及以上者晋级成功,否则晋级失败(满分100分). 
(1)求图中a的值;
(2)根据已知条件完成下面2×2列联表,并判断能否有85%的把握认为“晋级成功”与性别有关?
晋级成功 | 晋级失败 | 合计 | |
男 | 16 | ||
女 | 50 | ||
合计 |
(参考公式:K2= ![]() ,其中n=a+b+c+d)
,其中n=a+b+c+d)
P(K2≥k) | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
k | 0.780 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
(3)将频率视为概率,从本次考试的所有人员中,随机抽取4人进行约谈,记这4人中晋级失败的人数为X,求X的分布列与数学期望E(X).
【题目】(满分12分)学习雷锋精神前半年内某单位餐厅的固定餐椅经常有损坏,学习雷锋精神时全修好;单位对学习雷锋精神前后各半年内餐椅的损坏情况作了一个大致统计,具体数据如下:
损坏餐椅数 | 未损坏餐椅数 | 总 计 | |
学习雷锋精神前 | 50 | 150 | 200 |
学习雷锋精神后 | 30 | 170 | 200 |
总 计 | 80 | 320 | 400 |
(Ⅰ)求:学习雷锋精神前后餐椅损坏的百分比分别是多少?并初步判断损毁餐椅数量与学习雷锋精神是否有关?
(Ⅱ)请说明是否有97.5%以上的把握认为损毁餐椅数量与学习雷锋精神有关?
参考公式:![]() ,
,![]()
P(K2≥k0) | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |



