题目内容
如图,四棱锥P—ABCD的底面ABCD是边长为1的菱形,∠BCD﹦60°,E是CD中点,
PA⊥底面ABCD,PA=
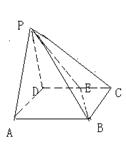
(1)证明:平面PBE⊥平面PAB
(2)求二面角A—BE—P的大小。
PA⊥底面ABCD,PA=


(1)证明:平面PBE⊥平面PAB
(2)求二面角A—BE—P的大小。
(1)略
(2)600
(1)连BD,由AB CD是菱形且∠BCD=600知△BCD是等边三角形。∵E中CD中点
CD是菱形且∠BCD=600知△BCD是等边三角形。∵E中CD中点
∴BE⊥CD 又AB∥CD,∴BE⊥AB (2分)
又∵PA⊥平面ABCD,BE 平面ABCD∴PA⊥BE (4分)
平面ABCD∴PA⊥BE (4分)
而PA∩AB=A ∴BE⊥平面PAB又BE 平面PBE ∴平面PBE⊥平面PAB(6分)
平面PBE ∴平面PBE⊥平面PAB(6分)
(2)由(1)知BE⊥平面PAB ∴BE⊥PB又BE⊥AB∴∠PBA是二面角A— BE—P的平面角 (9分)
BE—P的平面角 (9分)
在RT△PAB中,tan∠PBA=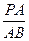 =
=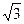 ∴∠PBA=600 (11分)
∴∠PBA=600 (11分)
故二面角A—BE—P的大小是600 (12分)
 CD是菱形且∠BCD=600知△BCD是等边三角形。∵E中CD中点
CD是菱形且∠BCD=600知△BCD是等边三角形。∵E中CD中点∴BE⊥CD 又AB∥CD,∴BE⊥AB (2分)
又∵PA⊥平面ABCD,BE
 平面ABCD∴PA⊥BE (4分)
平面ABCD∴PA⊥BE (4分)而PA∩AB=A ∴BE⊥平面PAB又BE
 平面PBE ∴平面PBE⊥平面PAB(6分)
平面PBE ∴平面PBE⊥平面PAB(6分)(2)由(1)知BE⊥平面PAB ∴BE⊥PB又BE⊥AB∴∠PBA是二面角A—
 BE—P的平面角 (9分)
BE—P的平面角 (9分)在RT△PAB中,tan∠PBA=
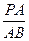 =
=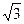 ∴∠PBA=600 (11分)
∴∠PBA=600 (11分)故二面角A—BE—P的大小是600 (12分)

练习册系列答案
相关题目
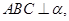
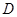 为
为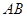 的中点,
的中点,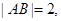
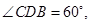
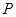 为
为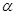 内的动点,且
内的动点,且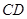 的距离为
的距离为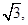 则
则 的最大值为
的最大值为 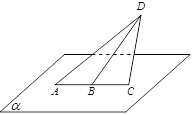
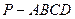 中,底面
中,底面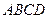 是直角梯形,
是直角梯形,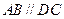 ,
,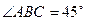 ,
,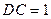 ,
,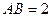 ,
,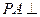 平面
平面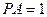 .
. 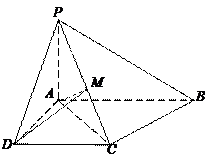
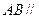 平面
平面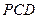 ;
;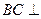 平面
平面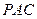 ;
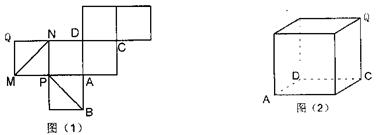
;
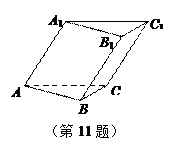
 的正方体ABCD-A1B1C1D1中
的正方体ABCD-A1B1C1D1中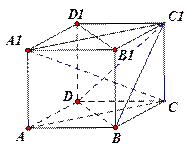
 ∥平面C1BD
∥平面C1BD 平面C1BD
平面C1BD 棱锥
棱锥 的底面
的底面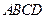 是
是 正方形,侧棱
正方形,侧棱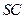 的中点
的中点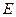 在底面内的射影恰好是正方形
在底面内的射影恰好是正方形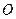 ,
, 顶点
顶点 在截面
在截面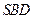 内
内 的射影恰好是
的射影恰好是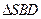 的重心
的重心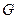 .
.
 与底面
与底面 ,求此四棱锥过点
,求此四棱锥过点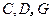 的截面面积.
的截面面积.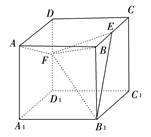
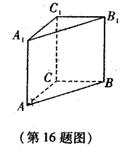
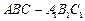 的所有棱长均等于1,且
的所有棱长均等于1,且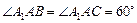 ,则该三棱柱的体积是
,则该三棱柱的体积是  ▲ .
▲ .