题目内容
【题目】已知椭圆E:![]() 过点(0,1)且离心率
过点(0,1)且离心率![]() .
.
(Ⅰ)求椭圆E的方程;
(Ⅱ)设动直线l与两定直线l1:x﹣y=0和l2:x+y=0分别交于P,Q两点.若直线l总与椭圆E有且只有一个公共点,试探究:△OPQ的面积是否存在最小值?若存在,求出该最小值;若不存在,说明理由.
【答案】(Ⅰ)![]() y2=1 (Ⅱ)存在,最小值为1
y2=1 (Ⅱ)存在,最小值为1
【解析】
(Ⅰ)由题意可得![]() ,根据离心率及
,根据离心率及![]() 间的关系即可求解 (Ⅱ)当直线l的斜率不存在时,易知S△OPQ
间的关系即可求解 (Ⅱ)当直线l的斜率不存在时,易知S△OPQ![]() ,当直线l的斜率存在时,设直线l:y=kx+m,k≠±1,根据点到直线的距离公式和三角形面积公式,借助函数的性质即可求出.
,当直线l的斜率存在时,设直线l:y=kx+m,k≠±1,根据点到直线的距离公式和三角形面积公式,借助函数的性质即可求出.
(Ⅰ)由已知得b=1,![]() ,a2=b2+c2,
,a2=b2+c2,
解得a![]() ,b=c=1,
,b=c=1,
所以椭圆的E方程为![]() y2=1,
y2=1,
(Ⅱ)当直线l的斜率不存在时,直线l为x![]() 或x
或x![]() ,
,
都有:S△OPQ![]() 2
2![]() 2.
2.
当直线l的斜率存在时,设直线l:y=kx+m,k≠±1,
由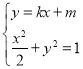 ,消去y,可得(1+2k2)x2+4kmx+2m2﹣2=0,
,消去y,可得(1+2k2)x2+4kmx+2m2﹣2=0,
∴△=﹣8m2+8+16k2,由题可知,△=0,有m2=2k2+1,
又 ![]() 可得P(
可得P(![]() ,
,![]() );同理可得Q(
);同理可得Q(![]() ,
,![]() ).
).
由原点O到直线PQ的距离为d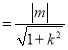 和|PQ|=2|m|
和|PQ|=2|m|![]() ,
,
可得S△OPQ![]() d|PQ|=|
d|PQ|=|![]() |,
|,
∵m2=2k2+1,
∴S△OPQ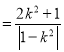 ,
,
当1﹣k2<0,即k>1或k<﹣1时,S△OPQ![]() 2
2![]() 2,
2,
当1﹣k2>0,即﹣1<k<1时,S△OPQ![]() 2
2![]() ,
,
因为0<1﹣k2≤1,
所以![]() 3,
3,
所以S△OPQ![]() 2
2![]() 1,当且仅当k=0时等号成立.
1,当且仅当k=0时等号成立.
综上,当k=0时,△OPQ的面积存在最小值为1.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目