题目内容
【题目】已知函数![]() ,
,![]() ,函数
,函数![]() ,记
,记![]() .把函数
.把函数![]() 的最大值
的最大值![]() 称为函数
称为函数![]() 的“线性拟合度”.
的“线性拟合度”.
(1)设函数![]() ,
,![]() ,
,![]() ,求此时函数
,求此时函数![]() 的“线性拟合度”
的“线性拟合度”![]() ;
;
(2)若函数![]() ,
,![]() 的值域为
的值域为![]() (
(![]() ),
),![]() ,求证:
,求证:![]() ;
;
(3)设![]() ,
,![]() ,求
,求![]() 的值,使得函数
的值,使得函数![]() 的“线性拟合度”
的“线性拟合度”![]() 最小,并求出
最小,并求出![]() 的最小值.
的最小值.
【答案】(1)![]() ;(2)证明见解析;(3)当
;(2)证明见解析;(3)当![]() 时,
时,![]() .
.
【解析】
(1)由题意,将![]() 和
和![]() 带入
带入![]() 求出
求出![]() 的表达式,求出此时
的表达式,求出此时![]() 的最大值即可;
的最大值即可;
(2)由定义写出![]() 的表达式,以及
的表达式,以及![]() 可能的取值情况,再用绝对值不等式性质即可得到所求;
可能的取值情况,再用绝对值不等式性质即可得到所求;
(3)写出![]() 的函数表达式,讨论
的函数表达式,讨论![]() 的不同取值情况时函数的单调性,求出其对应的
的不同取值情况时函数的单调性,求出其对应的![]() 值.
值.
(1)![]() ,
,
当![]() 时,
时,![]() ,
,
当且仅当![]() ,即
,即![]() 时,取等号,
时,取等号,
所以![]() ,则
,则![]() 在
在![]() 时单调递减,
时单调递减,
在![]() 时单调递增.
时单调递增.
又![]() ,
,![]() ,所以函数
,所以函数![]() 对于函数
对于函数![]() 的“线性拟合度”
的“线性拟合度”![]() ;
;
(2) 根据定义,![]() ,又
,又![]() ,
,
所以![]() ,
,![]() ,
,
于是![]() .
.
因为![]()
所以![]() ,即
,即![]() ;
;
(3)![]() ,
,![]() ,
,![]() ,
,
考虑函数![]() ,
,![]() 的值域:
的值域:
① 当![]() 时,
时,![]() 在
在![]() 时单调递增,
时单调递增,![]() ,
,
由(2)知,![]() ,
,
当![]() 时,取等号,故
时,取等号,故![]() 最小为
最小为![]() ;
;
② 当![]() 时,
时,![]() ,
,![]() ,
,
当![]() ,即
,即![]() 时,
时,![]() 在
在![]() 时单调递增,
时单调递增,![]() ,
,
由(2)知,![]() ,
,
当![]() 时,取等号,故
时,取等号,故![]() 最小为
最小为![]() ;;
;;
当![]() ,即
,即![]() 时,
时,![]() ,
,
由(2)知,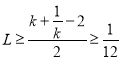 ,当且仅当
,当且仅当![]() 时取等号,
时取等号,![]() 最小为
最小为![]() ;
;
当![]() ,即
,即![]() 时,
时,![]() ,
,
由(2)知,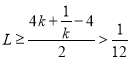 ;
;
当![]() ,即
,即![]() 时,
时,![]() 在
在![]() 时单调递减,
时单调递减,![]() ,
,
由(2)知,![]() .
.
综上,当且仅当![]() 时,
时,![]() .
.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目