题目内容
在正方体ABCD-A1B1C1D1中,
(1)求A1B1与AC所成角的大小;
(2)若E是A1C的中点,求证:BE⊥平面AB1C.
(1)求A1B1与AC所成角的大小;
(2)若E是A1C的中点,求证:BE⊥平面AB1C.
分析:(1)由于在正方体ABCD-A1B1C1D1中,AB∥A1B1,则A1B1与AC所成角的大小即为∠CAB=45°;
(2)根据DD1⊥AC,AC⊥BD,BD∩DD1=D,满足线面垂直的判定定理,则AC⊥平面BDD1,进而得到AC⊥BD1,同理AB1⊥BD1,
再根据线面垂直的判定定理可知BD1⊥平面AB1C.
(2)根据DD1⊥AC,AC⊥BD,BD∩DD1=D,满足线面垂直的判定定理,则AC⊥平面BDD1,进而得到AC⊥BD1,同理AB1⊥BD1,
再根据线面垂直的判定定理可知BD1⊥平面AB1C.
解答: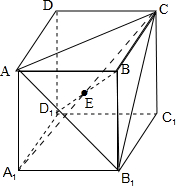 证明:(1)∵在正方体ABCD-A1B1C1D1中,AB∥A1B1,
证明:(1)∵在正方体ABCD-A1B1C1D1中,AB∥A1B1,
∴A1B1与AC所成角即为AB与AC所成角即∠CAB,
又∵∠CAB=45°,
∴A1B1与AC所成角为45°;
(2)连接BD1,∵E是A1C的中点,∴E也是BD1的中点,
∵在正方体ABCD-A1B1C1D1中,DD1⊥平面ABCD,
∴DD1⊥AC,
又∵AC⊥BD,BD∩DD1=D,
∴AC⊥平面BDD1,
又∵BD1?平面BDD1,
∴AC⊥BD1,同理AB1⊥BD1,
又∵AC∩AB1=A,
∴BD1⊥平面AB1C.
 证明:(1)∵在正方体ABCD-A1B1C1D1中,AB∥A1B1,
证明:(1)∵在正方体ABCD-A1B1C1D1中,AB∥A1B1,∴A1B1与AC所成角即为AB与AC所成角即∠CAB,
又∵∠CAB=45°,
∴A1B1与AC所成角为45°;
(2)连接BD1,∵E是A1C的中点,∴E也是BD1的中点,
∵在正方体ABCD-A1B1C1D1中,DD1⊥平面ABCD,
∴DD1⊥AC,
又∵AC⊥BD,BD∩DD1=D,
∴AC⊥平面BDD1,
又∵BD1?平面BDD1,
∴AC⊥BD1,同理AB1⊥BD1,
又∵AC∩AB1=A,
∴BD1⊥平面AB1C.
点评:本题考查异面直线所成的角,以及平面与平面垂直的判定,同时考查学生空间想象能力,逻辑思维能力,是中档题.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
 16、在正方体ABCD-A′B′C′D′中,过对角线BD′的一个平面交AA′于E,交CC′于F,则
16、在正方体ABCD-A′B′C′D′中,过对角线BD′的一个平面交AA′于E,交CC′于F,则
 如图,在正方体ABCD-A′B′C′D′中,E,F分别是AB′,BC′的中点.
如图,在正方体ABCD-A′B′C′D′中,E,F分别是AB′,BC′的中点.  如图在正方体ABCD-A 1B1C1D1中,O是底面ABCD的中心,B1H⊥D1O,H为垂足,则B1H与平面AD1C的位置关系是( )
如图在正方体ABCD-A 1B1C1D1中,O是底面ABCD的中心,B1H⊥D1O,H为垂足,则B1H与平面AD1C的位置关系是( )