题目内容
【题目】已知函数![]() 是定义在R上的偶函数,且当
是定义在R上的偶函数,且当![]() 时,
时,![]() (
(![]() ).
).
(1)当![]() 时,求
时,求![]() 的表达式:
的表达式:
(2)求![]() 在区间
在区间![]() 的最大值
的最大值![]() 的表达式;
的表达式;
(3)当![]() 时,若关于x的方程
时,若关于x的方程![]() (a,
(a,![]() )恰有10个不同实数解,求a的取值范围.
)恰有10个不同实数解,求a的取值范围.
【答案】(1)![]() ;(2)
;(2)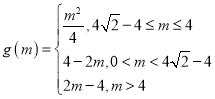 ;(3)
;(3)![]()
【解析】
(1)根据偶函数的特点,可知![]() ,可得结果.
,可得结果.
(2)采用分类讨论方法,![]() 与
与![]() ,去掉绝对值研究函数
,去掉绝对值研究函数![]() 在区间
在区间![]() 上的单调性,可得结果.
上的单调性,可得结果.
(3)画出函数![]() 图像,利用换元法
图像,利用换元法![]() ,得出
,得出![]() 与
与![]() ,可转化为
,可转化为![]() 两个根为
两个根为![]() ,可得
,可得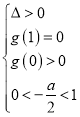 ,最后计算可得结果.
,最后计算可得结果.
(1)令![]() ,则
,则![]()
由当![]() 时,
时,![]()
所以![]()
又函数![]() 是定义在R上的偶函数,
是定义在R上的偶函数,
即![]()
所以![]()
所以当![]() 时,
时,![]()
(2)当![]() 时,
时,
如图
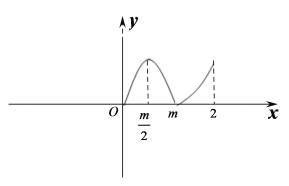
可知函数![]() 的最大值在
的最大值在![]() 或
或![]() 处取得,
处取得,
所以![]() ,
,![]()
![]()
![]()
①若![]() ,此时
,此时![]()
②若![]() ,此时
,此时![]() ;
;
当![]() 时,
时,![]() ,对称轴为
,对称轴为![]()
③若![]() ,即
,即![]() 时,则
时,则![]() ,
,
④若![]() ,即
,即![]() 时,则
时,则![]()
综上,得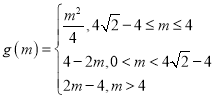
(3)当![]() 时,
时,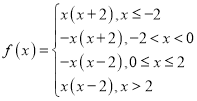
如图
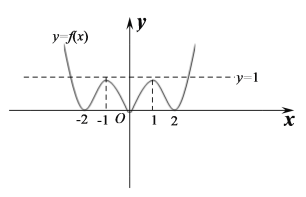
令![]()
由![]() 的图象可知,
的图象可知,
当![]() 时,方程
时,方程![]() 有两解;
有两解;
当![]() 时,方程
时,方程![]() 有四解;
有四解;
当![]() 时,方程
时,方程![]() 有六解;
有六解;
当![]() 时,方程
时,方程![]() 有三解;
有三解;
当![]() 时,方程
时,方程![]() 无解.
无解.
要使方程![]() (a,
(a,![]() )
)
恰有10个不同实数解,
则关于t的方程![]() 的一个根为1,
的一个根为1,
另一个根![]() ,设
,设![]() ,则有
,则有
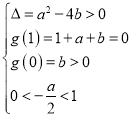
则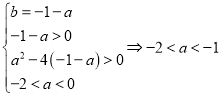
所以a的取值范围为![]() .
.

练习册系列答案
相关题目