题目内容
已知函数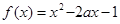 在区间
在区间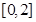 上的最大值为
上的最大值为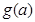 ,最小值为
,最小值为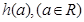 。
。
(1)求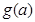 和
和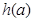 ;
;
(2)作出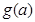 和
和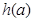 的图像,并分别指出
的图像,并分别指出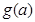 的最小值和
的最小值和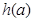 的最大值各为多少?
的最大值各为多少?
(1)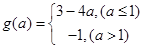 ,
,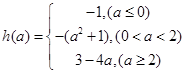 ;
;
(2)y=g(a)的最小值为-1; y=h(a)的最大值为-1。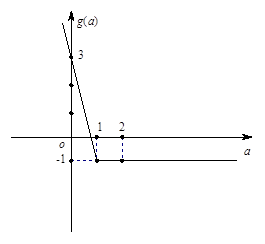
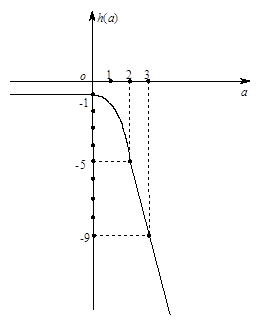
解析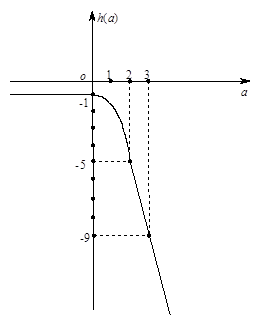
试题分析:(1).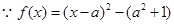 ,又
,又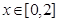 ;
;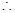 当
当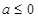 时,
时,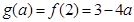 ,
,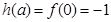 ;
;
当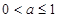 时,
时,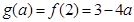 ,
,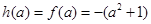 ;
;
当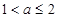 时,
时,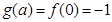 ,
,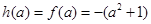 ;
;
当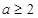 时,
时,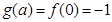 ,
,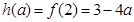 。
。
综上可知: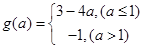 ,
, 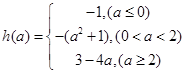 。
。
(2)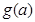 和
和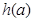 的图像分别为:
的图像分别为: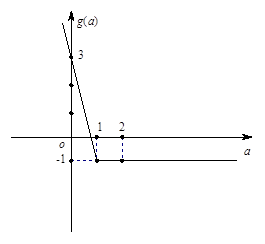
由图象可知,y=g(a)的最小值为-1。
由图象知,函数y=h(a)的最大值为-1。
考点:本题考查二次函数在闭区间上的最值和函数的图象。
点评:本题主要考查二次函数在闭区间上最值的求解,解题中注意应用分类讨论思想,其分类讨论的依据主要是:比较对称轴与区间的位置关系。

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
某企业为打入国际市场,决定从A、B两种产品中只选择一种进行投资生产.已
知投资生产这两种产品的有关数据如下表:(单位:万美元)
| 项目类别 | 年固定成本 | 每件产品成本 | 每件产品销售价 | 每年最多可生产的件数 |
| A产品 | 10 | m | 5 | 100 |
| B产品 | 20 | 4 | 9 | 60 |
(1)写出该厂分别投资生产A、B两种产品的年利润y1,y2与生产相应产品的件数x之间的函数关系并指明其定义域;
(2)如何投资才可获得最大年利润?请你做出规划.
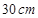 的
的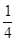 圆形(
圆形( 为圆心)铝皮上截取一块矩形材料
为圆心)铝皮上截取一块矩形材料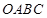 ,其中点
,其中点 在圆上,点
在圆上,点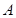 、
、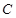 在两半径上,现将此矩形铝皮
在两半径上,现将此矩形铝皮 为母线的圆柱形罐子的侧面(不计剪裁和拼接损耗),设矩形的边长
为母线的圆柱形罐子的侧面(不计剪裁和拼接损耗),设矩形的边长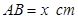 ,圆柱的体积为
,圆柱的体积为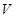
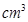 .
.
 的函数关系式,并指出定义域;
的函数关系式,并指出定义域; 米.
米.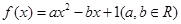 ,
,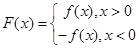
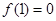 且对任意实数
且对任意实数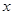 均有
均有 ,求
,求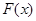 的解析式;
的解析式;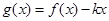 在区间
在区间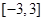 是单调函数,求实数
是单调函数,求实数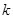 的取值范围;
的取值范围;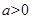 且
且 为偶函数,如果
为偶函数,如果 ,求证:
,求证: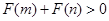 .
.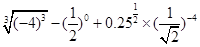 ;
;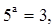
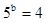 . 求a、b,并用
. 求a、b,并用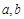 表示
表示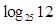 .
.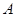 上市销售40天内全部售完,该公司对第一批产品
上市销售40天内全部售完,该公司对第一批产品
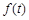 与第一批产品A上市时间t的关系式;
与第一批产品A上市时间t的关系式;