题目内容
在数列 中,
中,
(Ⅰ)求数列 的前
的前 项和
项和 ;
;
(Ⅱ)若存在 ,使得
,使得 成立,求实数
成立,求实数 的最小值.
的最小值.
(1) 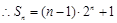 (2)
(2)  的最小值为
的最小值为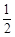
解析试题分析:(I) ……①
……①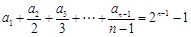 ②
②
由①—②得: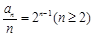
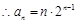 ,当
,当 时,也符合
时,也符合 ……③
……③
2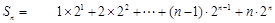 ……④
……④
又③—④得: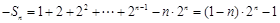
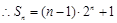 6分
6分
(II)由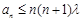 得
得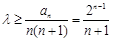
令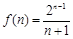

 单调递增,从而
单调递增,从而
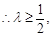 因此实数
因此实数 的最小值为
的最小值为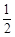 12分
12分
考点:数列的求和与函数单调性的运用
点评:解决的关键是对于数列的错位相减法的运用,以及函数的最值的考虑,属于基础题。

练习册系列答案
相关题目
 在函数
在函数 图象上,过点
图象上,过点 的切线的方向向量为
的切线的方向向量为 (
( >0).
>0). 的通项公式
的通项公式 ≤Sn对任意正整数n均成立,求实数
≤Sn对任意正整数n均成立,求实数 ,a1=1,点
,a1=1,点 在直线
在直线 上.
上. ,求证:
,求证: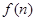 <1.
<1. }满足
}满足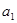 =1,
=1, =
= ,(1)计算
,(1)计算 ,
, ,
, 的值;(2)归纳推测
的值;(2)归纳推测 ,
, 为正整数.
为正整数. 和
和 的值;
的值; 的通项公式为
的通项公式为 (
( ),求数列
),求数列 ;
; 满足:
满足: ,
, ,设
,设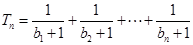 ,若(Ⅱ)中的
,若(Ⅱ)中的 恒成立,试求m的最大值.
恒成立,试求m的最大值. 是单调递增的等差数列,首项
是单调递增的等差数列,首项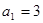 ,前
,前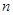 项和为
项和为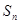 ,数列
,数列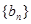 是等比数列,首项
是等比数列,首项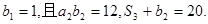
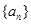 和
和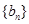 的通项公式.
的通项公式.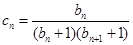 ,数列
,数列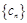 的前
的前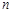 项和为
项和为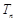 ,求证:
,求证: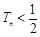 .
. 都是等差数列,且公差相等,(1)求
都是等差数列,且公差相等,(1)求 的通项公式;(2)若
的通项公式;(2)若 的前三项,记数列
的前三项,记数列 数列
数列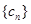 的前n项和为
的前n项和为
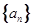 中,
中,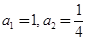 ,且
,且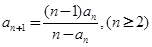 .
.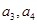 ,猜想
,猜想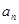 的表达式,并加以证明;
的表达式,并加以证明;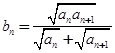 ,求证:对任意的自然数
,求证:对任意的自然数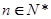 ,都有
,都有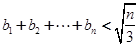 ;
;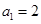 ,点
,点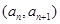 在函数
在函数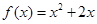 的图象上,其中
的图象上,其中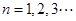
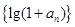 是等比数列;
是等比数列;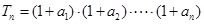 ,求
,求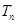 及数列
及数列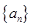 的通项;
的通项;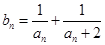 ,求数列
,求数列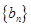 的前
的前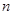 项和
项和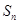 。
。