题目内容
【题目】已知函数f(x)=ax3+bx2+cx在点x0处取得极大值5,其导函数y=f′(x)的图象经过点(1,0),(2,0),如图所示.求: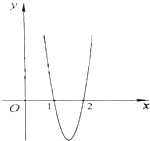
(1)x0的值;
(2)a,b,c的值.
(3)若曲线y=f(x)(0≤x≤2)与y=m有两个不同的交点,求实数m的取值范围.
【答案】
(1)解:由图象可知,在(﹣∞,1)上f'(x)>0,在(1,2)上f'(x)<0.
在(2,+∞)上f'(x)>0.
故f(x)在(﹣∞,1),(2,+∞)上递增,在(1,2)上递减.
因此f(x)在x=1处取得极大值,所以x0=1.
(2)解:f'(x)=3ax2+2bx+c,
由f'(1)=0,f'(2)=0,f(1)=5,
得 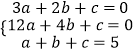 ,
,
解得a=2,b=﹣9,c=12
(3)解:由(1)知,函数在[0,1]上单调递增,在[1,2]上单调递减,
∵f(x)=2x3﹣9x2+12x,
∴f(0)=0,f(1)=5,f(2)=4,
∵y=f(x)(0≤x≤2)与y=m有两个不同的交点,
∴m∈[4,5).
【解析】(1)观察图象满足f′(x)=0的点附近的导数的符号的变化情况,来确定极大值,求出x0的值;(2)根据图象可得f'(1)=0,f'(2)=0,f(1)=5,建立三个方程,联立方程组求解即可;(3)由(1)知,函数在[0,1]上单调递增,在[1,2]上单调递减,求出相应函数值,即可求实数m的取值范围.
【考点精析】关于本题考查的利用导数研究函数的单调性和函数的极值与导数,需要了解一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值才能得出正确答案.
是极小值才能得出正确答案.

 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
