Question

【题目】已知△ABC中，点A（﹣2，0），B（2，0），C（x，1） （i）若∠ACB是直角，则x=
（ii）若△ABC是锐角三角形，则x的取值范围是 ．

Answer 1

【答案】；（﹣2，﹣ ）∪（2，+∞）
【解析】解：（i）∵△ABC中，点A（﹣2，0），B（2，0），C（x，1）， ∴ =（﹣2﹣x，﹣1）， =（2﹣x，﹣1），
∵∠ACB是直角，
∴ =（﹣2﹣x）（2﹣x）+（﹣1）（﹣1）=x2﹣3=0，
解得x= ．
（ii）∵△ABC中，点A（﹣2，0），B（2，0），C（x，1），
∴ =（﹣2﹣x，﹣1）， =（2﹣x，﹣1）， =（x+2，1）， =（4，0）， =（x﹣2，1）， =（﹣4，0），
∵△ABC是锐角三角形，
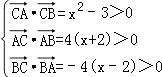∴ ，解得﹣2＜x＜﹣ 或x＞2．
∴x的取值范围是（﹣2，﹣ ）∪（2，+∞）．
故答案为： ，（﹣2，﹣ ）∪（2，+∞）．
（i）求出 =（﹣2﹣x，﹣1）， =（2﹣x，﹣1），由∠ACB是直角，则 =0，由此能求出x．
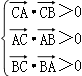（ii）分别求出 ， ， ， ， ， ，由△ABC是锐角三角形，得 ，由此能求出x的取值范围．