题目内容
(本题满分16分)
设正项等差数列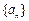 的前n项和为
的前n项和为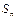 ,其中
,其中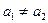 .
.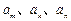 是数列
是数列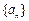 中满足
中满足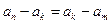 的任意项.
的任意项.
(1)求证: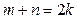 ;
;
(2)若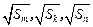 也成等差数列,且
也成等差数列,且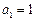 ,求数列
,求数列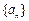 的通项公式;
的通项公式;
(3)求证: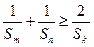 .
.
设正项等差数列
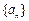 的前n项和为
的前n项和为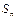 ,其中
,其中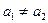 .
.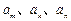 是数列
是数列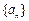 中满足
中满足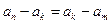 的任意项.
的任意项.(1)求证:
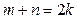 ;
;(2)若
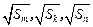 也成等差数列,且
也成等差数列,且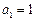 ,求数列
,求数列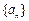 的通项公式;
的通项公式;(3)求证:
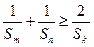 .
.(1)设等差数列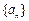 的公差为
的公差为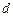 ,
,
因为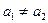 ,所以
,所以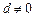 , ……..1分
, ……..1分
又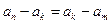 ,
,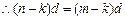 , ……..3分
, ……..3分
所以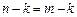 ,即
,即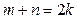 ; …..4分
; …..4分
(2)由已知取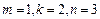 ,即
,即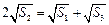 ……..6分
……..6分
把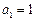 代入解得
代入解得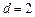 ,
,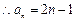 . ……..9分
. ……..9分
又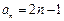 时,
时,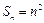 ,
,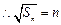
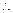 当
当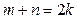 时,
时,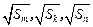 都成等差数列;
都成等差数列;
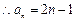 ; ……..10分
; ……..10分
(3)由条件得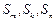 都大于0,
都大于0,
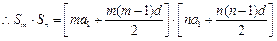
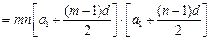
 ……..14分
……..14分
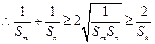 ,
,
即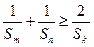 . ……..16分
. ……..16分
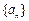 的公差为
的公差为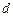 ,
,因为
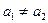 ,所以
,所以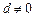 , ……..1分
, ……..1分又
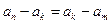 ,
,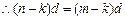 , ……..3分
, ……..3分所以
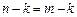 ,即
,即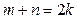 ; …..4分
; …..4分(2)由已知取
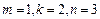 ,即
,即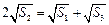 ……..6分
……..6分把
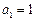 代入解得
代入解得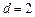 ,
,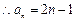 . ……..9分
. ……..9分又
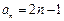 时,
时,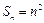 ,
,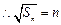
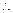 当
当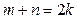 时,
时,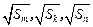 都成等差数列;
都成等差数列; 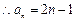 ; ……..10分
; ……..10分(3)由条件得
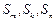 都大于0,
都大于0,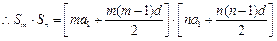
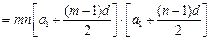
 ……..14分
……..14分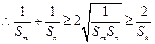 ,
,即
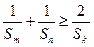 . ……..16分
. ……..16分略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
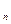 }满足S
}满足S
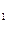 、a
、a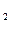 、a
、a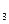 、a
、a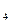 ,并由此猜想通项公式a
,并由此猜想通项公式a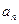 }是整数组成的数列,a1 = 1,且点
}是整数组成的数列,a1 = 1,且点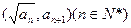 在函数
在函数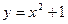 的图象上,
的图象上,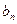 }满足
}满足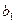 = 1,
= 1,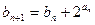 ,求证:
,求证: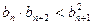
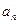 }中
}中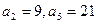 .
.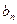 =
=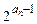 ,求数列
,求数列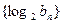 的前
的前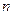 项和
项和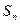 .
.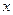 ,以后每次生成的结果可将上一次生成的每一个数
,以后每次生成的结果可将上一次生成的每一个数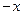 ,另一个是
,另一个是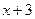 .设第
.设第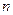 次生成的数的个数为
次生成的数的个数为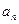 ,则数列
,则数列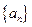 的前
的前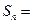 _________________;若
_________________;若 ,前
,前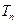 ,则
,则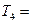 ______________________.
______________________.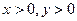 ,且
,且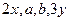 成等差数列,
成等差数列,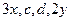 成等比数列,则
成等比数列,则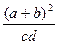 的最小值为 ( )
的最小值为 ( )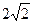
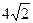
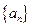 中,
中,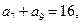
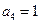 ,则
,则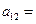
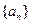 中,
中,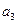 =2,
=2,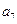 =1,若
=1,若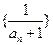 为等差数列,则
为等差数列,则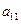 等于( )
等于( )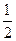
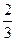
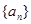 中,
中,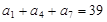 ,
,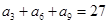 ,则数列
,则数列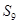 等于( )
等于( )


