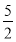题目内容
11.(1)讨论m取不同的值时,函数f(x)=$\frac{2}{{3}^{x}-1}$+m的奇偶性;(2)画出函数y=|3x-1|的图象,并利用图象方程|3x-1|=k解得个数.(作图请用尺)
分析 (1)先求函数f(x)=$\frac{2}{{3}^{x}-1}$+m的定义域,再求f(-x)=$\frac{2}{{3}^{-x}-1}$+m=$\frac{-2•{3}^{x}}{{3}^{x}-1}$+m;从而确定f(-x)与f(x)的关系即可.
(2)作出函数y=|3x-1|的图象,由图象写出方程|3x-1|=k解得个数即可.
解答 解:(1)函数f(x)=$\frac{2}{{3}^{x}-1}$+m的定义域为{x|x≠0},
f(-x)=$\frac{2}{{3}^{-x}-1}$+m=$\frac{-2•{3}^{x}}{{3}^{x}-1}$+m;
令f(x)+f(-x)=-2+2m=0得,
m=1;
故当m=1时,
函数f(x)=$\frac{2}{{3}^{x}-1}$+m是奇函数,
当m≠1时,
函数f(x)=$\frac{2}{{3}^{x}-1}$+m是非奇非偶函数.
(2)函数y=|3x-1|的图象如下,
故当k=0或k≥1时,方程|3x-1|=k只有一个解,
当0<k<1时,方程|3x-1|=k有两个解,
当k<0时,方程无解.
点评 本题考查了函数的奇偶性的判断与函数的图象的作法与应用,属于中档题.

练习册系列答案
相关题目
16.在平面直角坐标系中,已知点A,B在抛物线y2=4x上,且满足$\overrightarrow{OA}$•$\overrightarrow{OB}$=-4,点F是抛物线的焦点,设△OFA,△OFB的面积分别是S1,S2,那么S1•S2等于( )
| A. | 2 | B. | $\frac{5}{2}$ | C. | 3 | D. | 4 |
20.已知i为虚数单位,复数z=a+bi(a,b∈R)的虚部b记作Im(z),则Im($\frac{1}{1+i}$)=( )
| A. | -$\frac{1}{2}$ | B. | -1 | C. | $\frac{1}{2}$ | D. | 1 |
1.如图复平面内的点A表示复数z,则复数$\frac{z}{1+i}$表示的点所在的象限为( )


| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
 的单调减区间为 .
的单调减区间为 . ,且
,且 分别为
分别为 的三边
的三边 所对的角.
所对的角. 的大小;
的大小; 成等差数列,且
成等差数列,且 ,求
,求 边的长.
边的长. ,若向量
,若向量 与
与 平行,则
平行,则 ( )
( ) B.
B.
 D.
D.