题目内容
16.在平面直角坐标系中,已知点A,B在抛物线y2=4x上,且满足$\overrightarrow{OA}$•$\overrightarrow{OB}$=-4,点F是抛物线的焦点,设△OFA,△OFB的面积分别是S1,S2,那么S1•S2等于( )| A. | 2 | B. | $\frac{5}{2}$ | C. | 3 | D. | 4 |
分析 设l过A、B的方程为:x=ty+b代入抛物线y2=4x,消去x,通过$\overrightarrow{OA}$•$\overrightarrow{OB}$=-4,得到直线恒过的定点,判断出A、B的位置,然后求出结果即可.
解答 解:设l过A、B的方程为:x=ty+b代入抛物线y2=4x,消去x得
y2-4ty-4b=0,
设A(x1,y1),B(x2,y2),
则y1+y2=4t,y1y2=-4b,
∴$\overrightarrow{OA}$•$\overrightarrow{OB}$=(ty1+b)(ty2+b)+y1y2
=t2y1y2+bt(y1+y2)+b2+y1y2
=-4bt2+4bt2+b2-4b=b2-4b,
令b2-4b=-4,∴b2-4b+4=0∴b=2.
∴直线l过定点(2,0).
当x=2时,y=±2$\sqrt{2}$,此时|y1y2|取得最小值8,
∴S△OFA•S△OFB=$\frac{1}{2}$×1×$\frac{1}{2}$×1×|y1y2|=$\frac{1}{4}$×8=2.
故选A.
点评 本题考查直线与抛物线的位置关系,三角形的面积的求法,考查转化思想以及计算能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.已知抛物线C:y2=8x的焦点为F,点M(-1,0),不垂直于x轴的直线于抛物线相交于A,B两点,若x轴平分∠AMB,则△FAB的面积的取值范围是( )
| A. | (2$\sqrt{2}$,+∞) | B. | [2$\sqrt{2}$,+∞) | C. | (4$\sqrt{2}$,+∞) | D. | [4$\sqrt{2}$,+∞) |
 ,
,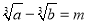 ,
,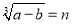 ,则有( )
,则有( )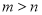 B.
B.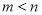
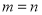 D.
D.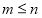
 为
为 内一点,满足
内一点,满足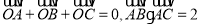 ,且
,且 ,则
,则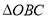 的面积为____________.
的面积为____________.