题目内容
11. 某几何体的三视图如图所示,P是正方形ABCD对角线的交点,G是PB的中点.
某几何体的三视图如图所示,P是正方形ABCD对角线的交点,G是PB的中点.(1)根据三视图,画出该几何体的直观图;
(2)在直观图中,①证明PD∥面AGC;②求此几何体的侧面积.
分析 (Ⅰ)根据三视图,可得该几何体为正四棱锥P-ABCD,正方形ABCD的边长为2,正四棱锥的高为$\sqrt{2}$,由此可得该几何体的直观图.
(Ⅱ)①在直观图中,设正方形ABCD的中心为O,利用三角形的中位线证明OG∥PD.再由直线和平面平行的判定定理证得 PD∥面AGC.
②连接PO,则PO⊥平面ABCD,取BC的中点E,连接PE,PE,则PE⊥BC,即可求此几何体的侧面积.
解答 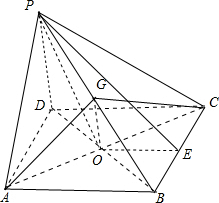 解:(1)根据三视图,可得该几何体为正四棱锥P-ABCD,正方形ABCD的边长为2,正四棱锥的高为$\sqrt{2}$,
解:(1)根据三视图,可得该几何体为正四棱锥P-ABCD,正方形ABCD的边长为2,正四棱锥的高为$\sqrt{2}$,
该几何体的直观图如图所示:
(2)①证明:在直观图中,设正方形ABCD的中心为O,
∵G是PB的中点,
∴OG是△PAD的中位线,故有OG∥PD.
而OG?面AGC,PD?面AGC,∴PD∥面AGC.
②连接PO,则PO⊥平面ABCD,
取BC的中点E,连接PE,PE,则PE⊥BC,
Rt△POE中,PO=$\sqrt{2}$,OE=1,
∴PE=$\sqrt{3}$,
∴几何体的侧面积S=4×$\frac{1}{2}×2×\sqrt{3}$=4$\sqrt{3}$.
点评 本题主要考查三视图、直线和平面平行的判定定理、直线和平面垂直的判定定理、平面和平面垂直的判定定理的应用,属于中档题.

练习册系列答案
相关题目
2.若奇函数f(x)对于任意的x1,x2∈(-∞,0]都有(x1-x2)[f(x1)-f(x2)]<0,则不等式f(lgx)+f(1)>0的解集为( )
| A. | $({0,\frac{1}{10}})$ | B. | (0,1) | C. | $(\frac{1}{10},1)$ | D. | (1,10) |
16.$\frac{2cos80°+cos160°}{cos70°}$的值是( )
| A. | -$\frac{1}{2}$ | B. | -$\frac{\sqrt{3}}{2}$ | C. | -$\sqrt{3}$ | D. | -$\sqrt{2}$ |
 已知△OAB中,$\overrightarrow{AM}$=$\overrightarrow{MB}$,$\overrightarrow{OG}$=2$\overrightarrow{GM}$,P、Q分别是边OA、OB上的动点,且$\overrightarrow{PG}$=λ$\overrightarrow{GQ}$(λ∈R),设$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OP}$=x$\overrightarrow{a}$,$\overrightarrow{OQ}$=y$\overrightarrow{b}$,(x∈R,y∈R)
已知△OAB中,$\overrightarrow{AM}$=$\overrightarrow{MB}$,$\overrightarrow{OG}$=2$\overrightarrow{GM}$,P、Q分别是边OA、OB上的动点,且$\overrightarrow{PG}$=λ$\overrightarrow{GQ}$(λ∈R),设$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OP}$=x$\overrightarrow{a}$,$\overrightarrow{OQ}$=y$\overrightarrow{b}$,(x∈R,y∈R)