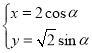题目内容
【题目】在数列{an}，{bn}中，an＝bn+n，bn＝﹣an+1.
（1）证明：数列{an+3bn}是等差数列.
（2）求数列
的前n项和Sn.
【答案】（1）证明见解析；（2）Sn
【解析】
（1）可将bn＝﹣an+1代入an＝bn+n计算可得数列{an}的通项公式，然后根据bn＝﹣an+1可得数列{bn}的通项公式，即可计算出数列{an+3bn}的通项公式，再根据等差数列的定义法可证明数列{an+3bn}是等差数列；
（2）先根据（1）的结果计算出数列
的通项公式，然后根据通项公式的特点可采用错位相减法计算出前n项和Sn.
（1）证明：由题意，将bn＝﹣an+1代入an＝bn+n，可得
an＝bn+n＝﹣an+1+n，即2an＝n+1，
∴an
，n∈N*，
∴bn＝﹣an+1
1
，n∈N*，
∴an+3bn
3
2﹣n，
∵（an+1+3bn+1）﹣（an+3bn）＝2﹣（n+1）﹣（2﹣n）＝﹣1，
∴数列{an+3bn}是以﹣1为公差的等差数列.
（2）由（1）知，
，
则Sn
，
∴
Sn
，
两式相减，可得
Sn
（
）
，/span>
∴Sn
.
【题目】为了贯彻落实党中央对新冠肺炎疫情防控工作的部署和要求，坚决防范疫情向校园蔓延，切实保障广大师生身体健康和生命的安全，教育主管部门决定通过电视频道、网络平台等多种方式实施线上教育教学工作.某教育机构为了了解人们对其数学网课授课方式的满意度，从经济不发达的A城市和经济发达的B城市分别随机调查了20个用户，得到了一个用户满意度评分的样本，并绘制出茎叶图如下：
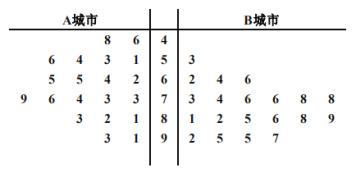
若评分不低于80分，则认为该用户对此教育机构授课方式“认可”，否则认为该用户对此教育机构授课方式“不认可”.
（1）请根据此样本完成下列2×2列联表，并据此列联表分析，能否有95%的把握认为城市经济状况与该市的用户认可该教育机构授课方式有关？
认可 | 不认可 | 合计 | |
A城市 | |||
B城市 | |||
合计 |
（2）以该样本中A，B城市的用户对此教育机构授课方式“认可”的频率分别作为A，B城市用户对此教育机构授课方式“认可”的概率.现从A城市和B城市的所有用户中分别随机抽取2个用户，用X表示这4个用户中对此教育机构授课方式“认可”的用户个数，求X的分布列.
参考公式：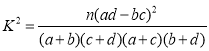
，其中
.
参考数据：
| 0.10 | 0.05 | 0.025 |
| 2.706 | 3.841 | 5.024 |
