题目内容
袋中有6个球,其中4个白球,2个红球,从袋中任意取出两球,求下列事件的概率:
(1)A:取出的两球都是白球;
(2)B:取出的两球1个是白球,另1个是红球.
(1)A:取出的两球都是白球;
(2)B:取出的两球1个是白球,另1个是红球.
(1)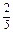 (2)
(2)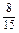
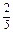 (2)
(2)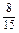
设4个白球的编号为1,2,3,4,2个红球的编号为5,6.
从袋中的6个小球中任取两个的方法为(1,2),(1,3),(1,4),(1,5),(1,6),(2,3),(2,4),(2,5),(2,6),(3,4),(3,5),(3,6),(4,5),(4,6),(5,6)共15个.
(1)从袋中的6个球中任取两个,所取的两球全是白球的总数,即是从4个白球中任取两个的方法总数,共有6个,即为(1,2),(1,3),(1,4),(2,3),(2,4),(3,4).
∴取出的两个球全是白球的概率为P(A)=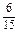 =
=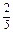 .
.
(2)从袋中的6个球中任取两个,其中1个为红球,而另1个为白球,其取法包括(1,5),(1,6),
(2,5),(2,6),(3,5),(3,6),(4,5),(4,6)共8个.
∴取出的两个球1个是白球,另1个是红球的概率
P(B)=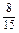 .
.
从袋中的6个小球中任取两个的方法为(1,2),(1,3),(1,4),(1,5),(1,6),(2,3),(2,4),(2,5),(2,6),(3,4),(3,5),(3,6),(4,5),(4,6),(5,6)共15个.
(1)从袋中的6个球中任取两个,所取的两球全是白球的总数,即是从4个白球中任取两个的方法总数,共有6个,即为(1,2),(1,3),(1,4),(2,3),(2,4),(3,4).
∴取出的两个球全是白球的概率为P(A)=
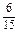 =
=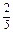 .
.(2)从袋中的6个球中任取两个,其中1个为红球,而另1个为白球,其取法包括(1,5),(1,6),
(2,5),(2,6),(3,5),(3,6),(4,5),(4,6)共8个.
∴取出的两个球1个是白球,另1个是红球的概率
P(B)=
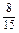 .
.
练习册系列答案
相关题目
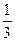

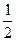
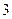 部分构成,这
部分构成,这
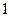 部分是黑色并且第
部分是黑色并且第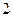 部分是红色.
部分是红色.
