题目内容
7．等差数列{an}的通项公式an=2n+1，其前n项和为Sn，则数列{$\frac{{S}_{n}}{n}$}的前4项的和为（ ）| A． | 20 | B． | 17 | C． | 16 | D． | 18 |
分析 根据题意，由等差数列的前n项和公式，可得Sn=$\frac{n（3+2n+1）}{2}$=n（n+2），进而可得 $\frac{{S}_{n}}{n}$=n+2，分析可得数列{ $\frac{{S}_{n}}{n}$}也是等差数列，且其通项公式为则 $\frac{{S}_{n}}{n}$=n+2，由等差数列的前n项和公式，计算可得答案．
解答 解：根据题意，等差数列{an}的通项公式an=2n+1，
则其首项为3，公差为2，
其前n项和为Sn=$\frac{n（3+2n+1）}{2}$=n（n+2），
则$\frac{{S}_{n}}{n}$=n+2，
数列{$\frac{{S}_{n}}{n}$}也是等差数列，且其通项公式为则$\frac{{S}_{n}}{n}$=n+2，
有a1=3，a4=6，
则其前4项的和为$\frac{4（3+6）}{2}$=18；
故选：D．
点评 本题考查数列的求和，关键是求出数列{ $\frac{{S}_{n}}{n}$}的通项，推出数列的性质，进而选择合适的求和公式．
练习册系列答案
相关题目
三棱锥P-ABC中，PA⊥平面ABC，AC⊥BC，D为侧棱PC上一点，它的正视图和侧视图 （如下图所示），则AD与平面PBC所成角的大小为$\frac{π}{2}$；三棱锥D-ABC的体积为$\frac{16}{3}$．
12．设等比数列{an}的首项a1=$\frac{1}{3}$，前n项和为Sn，若S1、2S2、3S3成等差数列，则{an}的通项为（ ）
| A． | an=$\frac{1}{{3}^{n}}$ | B． | an=3n | C． | an=$\frac{1}{{3}^{n-1}}$ | D． | an=$\frac{1}{{3}^{1-n}}$ |
19．已知抛物线方程为y=4x2，则该抛物线的焦点坐标为（ ）
| A． | （0，1） | B． | $（0，\frac{1}{16}）$ | C． | （1，0） | D． | $（\frac{1}{16}，0）$ |
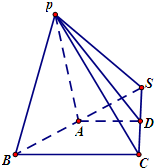在三棱锥P-SBC中，A，D分别为边SB，SC的中点，AB=2，BC=4，CD=2$\sqrt{2}$．平面PSB⊥平面ABCD，平面PAD⊥平面ABCD．