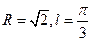题目内容
设向量 ,
, ,
,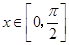 .
.
(1)若 ,求
,求 的值;
的值;
(2)设函数 ,求
,求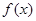 的最大值.
的最大值.
 ,
, ,
,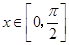 .
.(1)若
 ,求
,求 的值;
的值;(2)设函数
 ,求
,求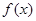 的最大值.
的最大值.(1) 的值为
的值为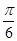 ;(2)
;(2)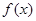 的最大值为
的最大值为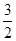 .
.
 的值为
的值为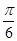 ;(2)
;(2)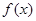 的最大值为
的最大值为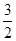 .
.试题分析:(1)去除向量的包装外衣,转化为由三角函数值求对应的角的值;(2)去除向量的包装外衣,转化为形如:
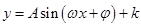 三角函数最值,但一定要关注自变量
三角函数最值,但一定要关注自变量 的范围.另外三角函数与代数函数一个很大的区别就是一般先要处理三角函数表达式,处理的结果之一就是转化为形如:
的范围.另外三角函数与代数函数一个很大的区别就是一般先要处理三角函数表达式,处理的结果之一就是转化为形如: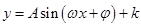 ,这一点很重要.
,这一点很重要.试题解析:(1)由
 得
得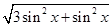
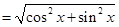 ,即
,即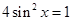 ,
,又∵
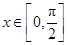 ,∴
,∴ ,从而
,从而 . (5分)
. (5分)(2)
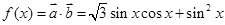
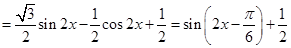 ,
,又∵
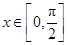 ,∴
,∴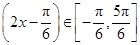 ,即有
,即有 ,所以
,所以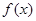 的最大值为
的最大值为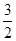 . (14分)
. (14分)
练习册系列答案
相关题目
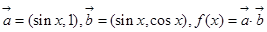
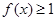 ,求x的范围;
,求x的范围;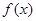 的最大值以及此时x的值.
的最大值以及此时x的值. ,
,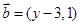 (
(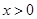 ,
, ),若
),若 ∥
∥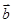 ,则
,则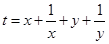 的最小
的最小 ⊥
⊥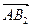 ,|
,|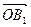 |=|
|=| |=1,
|=1, =
= |<
|<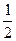 ,则|
,则| |的取值范围是( )
|的取值范围是( )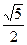 ]
] ]
] ]
] 中,
中, 分别是
分别是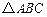 ,
,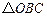 的重心,设
的重心,设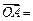
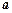 ,
,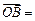
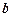 ,
,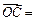
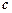 ,试用向量
,试用向量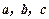 表示向量
表示向量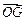 和
和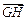 .
.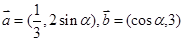 ,且
,且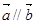 .若
.若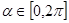 , 则
, 则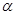 的值为
的值为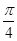
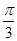
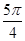
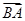 =(2,3),
=(2,3),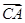 =(4,7),则
=(4,7),则 =( )
=( ) 、
、 ,则该球的半径R及点A、B在该球面上的最短距离
,则该球的半径R及点A、B在该球面上的最短距离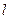 分别为
分别为 B.
B.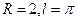 C.
C. D.
D.